array型の要素の次元と並び方はC言語風で一番後ろからメモリに配置される。Fortranとは逆なので注意。
行列の場合はa[行,列]になる?。GrADS形式のバイナリだったらFortranなら(x,y,z,t)だがNumPyで頭から読むと[t,z,y,x]になる。
- NumPy、Cの場合。
| a[0,0] | a[0,1] | a[0,2] | a[1,0] | a[1,1] | a[1,2] |
- Fortranの場合
| a(1,1) | a(2,1) | a(3,1) | a(1,2) | a(2,2) | a(3,2) |
要素の最も上位の型になる(複数の型が使えるstructured arrayというのもある)。dtypeで指定することもできる。指定方法は、
- NumPyの組み込み型(こちらの24種)。
- Python組み込み型(float、intとか)
- One-character strings
#組み込み型 a = np.array([1,2,3], dtype=np.int) #int型。32ビットマシンならint32、64ビットマシンならint64になるらしい。 b = np.array([1,2,3], dtype=np.float64) #8バイト浮動小数点 c = np.array([1,-1,1], dtype=np.bool) #bool型 #Python組み込み型 d = np.array([1,2,3], dtype=float) #浮動小数点 e = np.array(['T'], dtype=str) #文字型 #組み込み型はアルファベットでも指定できる。 f = np.array([1,2,3], dtype='<f') #リトルエンディアン単精度浮動小数点 g = np.array([1,2,3], dtype='>d') #ビッグエンディアン倍精度浮動小数点 #バイト数で指定することもできる。 h = np.array([1,2,3], dtype='<f32') #リトルエンディアン32ビット浮動小数点 i = np.array(['abc'], dtype='a3') #3文字の文字型
公式レファレンス
np.array([[1,2,3],[1,2,3]],dtype='float64') #リストから作成(※浮動小数点型) np.arange(5) #単調増加する1次元配列を作成 np.arange(0,5,0.5) #0から4.5まで0.5刻み np.linspace(1.,4.,6,endpoint=False) #区間を分割して作成(※終点は含まない) np.empty([2,2]) #任意のサイズの配列(値は適当) np.zeros([2,2]) #要素がゼロの配列 np.ones([2,2]) #要素が1の配列 np.identity(2) #単位行列
インデキシングやプロットの際に座標を表すような多次元配列が必要になる場合がある。
x = np.arange(-10,10.1,1) y = np.arange(-5, 5.1, 1) X, Y = np.meshgrid(x, y)
返り値があるメソッドであっても、変形した配列のコピーを返すものと、変形はするが値が保持されているものがあるので注意が必要。リファレンス
| 結合 | 分割 | 使い方 | |
|---|---|---|---|
| hstack | hsplit | np.hstack( (a,b) ) | 0軸(行ベクトル)にそって結合/分割 |
| vstack | vsplit | np.vstack( (a,b) ) | 1軸(列ベクトル)にそって結合/分割 |
| dstack | dsplit | np.dstack( (a,b) ) | 2軸にそって結合/分割 |
| concatenate | split | np.concatenate( (a,b),axis=0 ) | 指定した軸にそって結合/分割 |
- 結合する
>>> x #(2, 3)配列
array([[ 1, 2, 3],
[-1, -2, -3]])
>>> y #(2, 2)配列
array([[0, 1],
[1, 2]])
>>> z #(3, )配列
array([0, 0, 0])
>>> np.hstack((x, y)) #xとyを0軸(行)に沿って結合
array([[ 1, 2, 3, 0, 1],
[-1, -2, -3, 1, 2]])
2次元配列の場合はnp.c_やnp.r_のコンストラクタを使ってもできる。np.c_では1次元配列の場合は自動的に列ベクトルに変換されるので便利。
>>> a
array([1, 2, 3, 4])
>>> b
array([[11, 15],
[12, 16],
[13, 17],
[14, 18]])
>>> np.r_[a,1] #1軸にそってaにスカラー1を結合
array([1, 2, 3, 4, 1])
>>> np.c_[a,b] #2軸にそってaとbを結合。aに2軸はないので列ベクトルに変換される。
array([[ 1, 11, 15],
[ 2, 12, 16],
[ 3, 13, 17],
[ 4, 14, 18]])
指定した軸方向に要素を繰り返した配列を返す。軸を指定しない場合は1次元につぶして返す。tileはarrayを繰り返し、repeatは要素を繰り返す。
>>> np.tile(np.arange(5), 2) array([0, 1, 2, 3, 4, 0, 1, 2, 3, 4]) >>> np.repeat(np.arange(5),2) array([0, 0, 1, 1, 2, 2, 3, 3, 4, 4])repeatは軸を指定できる。指定しない場合は1次元にreshapeされてからrepeatされる。
>>> x
array([[0, 1, 2],
[3, 4, 5]])
>>> np.repeat(x, 2, axis=1) #1軸[0,1,2]と[3,4,5]の要素に対してrepeat
array([[0, 0, 1, 1, 2, 2],
[3, 3, 4, 4, 5, 5]])
>>> np.repeat(x, 2, axis=0) #0軸の要素[0,1,2]、[3,4,5]を繰り返す要素としてrepeat
array([[0, 1, 2],
[0, 1, 2],
[3, 4, 5],
[3, 4, 5]])
tileはそれぞれの軸の繰り返し回数を指定できる。入力配列の次元より大きい場合は前方に1が自動的に加えられる。repeatとの違いは要素ではなく配列全体を繰り返すところ。
>>> np.tile(x, (2,1)) #0軸方向に2回tileする。
array([[0, 1, 2],
[3, 4, 5],
[0, 1, 2],
[3, 4, 5]])
newaxisと合わしてブロードキャストのようなことができる。
>>> z = np.repeat(x[:, np.newaxis, :], 5, axis=1) #newaxisを入れた軸にそってリピート
>>> z.shape
(2, 5, 3)
>>> z[:, 0, :] #newaxisを入れた軸方向のスライスは金太郎飴のように繰り返し=ブロードキャストされる
array([[0, 1, 2],
[3, 4, 5]])
>>> z[:, 4, :]
array([[0, 1, 2],
[3, 4, 5]])
この場合newaxisをいれた軸の要素はゼロなのでtileでも同じ結果になる。上記の例はz = np.tile(x[:, np.newaxis, :], (1,5,1))と同じ。
| np.delete(x, idx, axis) | 要素を削除 |
|---|---|
| np.insert(x, idx, val, axis) | 要素を挿入 |
| np.append(x, idx, val, axis) | 要素を最後に追加 |
>>> x
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
#配列xの0軸に沿った1番目の要素を削除。すなわちx[1, :]を削除
>>> np.deleate(x, 1, 0)
array([[ 1, 2, 3, 4],
[ 9, 10, 11, 12]])
#スライスで指定することもできる。
>>> np.deleate(x, np.s_[::2], 1) #x[:, ::2]を削除
a = np.array([[1,2,3], [4,5,6]])
>>> np.reshape(a, 6) #形状の変更
array([1, 2, 3, 4, 5, 6])
>>> a.reshape(3,2) #メソッドも可
array([[1, 2],
[3, 4],
[5, 6]])
| reshape | 形状をタプル(1次元なら整数)で与えて形状を変更する。全体のサイズは変わらない。次元の一つを-1で指定すると全体のサイズが保たれるように自動調整される。メソッドとしても使える。 |
|---|---|
| ravel | 1次元に形状変更する。reshape(-1)と同じ。 |
| flatten | 1次元に形状変更した配列のコピーを返す。 |
| squeeze | 要素数1の次元を削除 |
>>> x = np.arange(1, 7).reshape(2, 3)
>>> x
array([[1, 2, 3],
[4, 5, 6]])
>>> y = x.ravel(); z = x.flatten()
>>> y, z
(array([1, 2, 3, 4, 5, 6]), array([1, 2, 3, 4, 5, 6]))
>>> z[0] = -1
>>> x
array([[1, 2, 3],
[4, 5, 6]])
>>> y[0] = -1
>>> x
array([[-1, 2, 3],
[4, 5, 6]])
>>> a = np.array(24).reshape(2,3,4) >>> a.shape (2, 3, 4) >>> a.T.shape #転置(次元を逆順で並べ替える) (4, 3, 2) >>> np.transpose(a, (1,2,0)).shape #0軸を1軸、1軸を2軸に、2軸を0軸に入れ替えるように転置する。 (3, 4, 2)
| ndarray.T | 転置したビューを返す。 |
|---|---|
| transpose(a, axes=None) | 転置したビューを返す。入れ替える軸の位置をタプルで与えて指定できる。 |
| rollaxis(a, axis, start=0) | 指定した軸を第3引数の次元の前に移動させる。 |
| swapaxes(a, axis1, axis2) | 指定した軸を入れ替える。 |
加減乗除などの演算子による演算、np.exp、np.sqrtなどのnumpyの関数は配列に対しては要素ごとに計算されるuniversal functionになっている。一覧はドキュメントを参照。
>>> a = np.array([1,2]) >>> b = np.array([2,3]) >>> a*b. array([2, 6]) >>> np.exp(a) array([ 2.71828183, 7.3890561 ]) >>> np.add(a, b) #a+bと同じ array([3, 5])
2つの引数をとるuniversal function(add、multiplyなど)には4つのメソッドがある。
例を述べる方が分かりやすい
| ufunc.reduce | 指定した次元(デフォルトは第一次元)に沿ってufuncを適用し次元を縮約する |
|---|---|
| ufunc.accumulate | 指定した次元(デフォルトは第一次元)に沿ってufuncを順に適用した累積結果を計算する |
| ufunc.outer | 2つの配列を引数にとってそのとり得るすべての要素のペアにufuncを適用した結果を返す(直積) |
| ufunc.reduceat | ufunc.reduceを指定したインデックスのスライスに対して指定した軸に沿って局所的に適用する |
ある軸に沿って演算をして次元を縮約する。例えば緯度に沿って1周足すとかで使える。
>>> a = np.arange(6).reshape(2,3)
>>> a
array([[0, 1, 2],
[3, 4, 5]])
>>> np.add.reduce(a)
array([3, 5, 7]) #[0+3, 1+4, 2+5]
>>> np.sum(a, axis=0) #これと同じ
array([3, 5, 7])
#要素数を求めるのにもつかえるかも。
>>> x.shape
(2, 5, 3)
>>> np.multiply.reduce(x)
30
reduceの途中経過みたいな感じか。
>>> np.add.accumulate(a)
array([[0, 1, 2], #[[0, 1, 2],
[3, 5, 7]]) [0+3, 1+4, 2+5]]
reduceatは分かりにくい。ドキュメントによるとnp.ufunc.reduceat(x, indices)は、
- iを0からlen(indices)まで回してxのスライスx[indices[i]:indices[i+1]]に対してufunc.add.reduceを演算していく。
- indices[i] >= indices[i+1]のときはx[indices[i]]になる。
- 最後はx[indices[i+1]:]になる。
>>> x = np.arange(6) >>> x array([0, 1, 2, 3, 4]) #ufunc.add.reduceatを使う場合。 >>> y = np.add.reduceat(x,[0,4,1,3]) #x[0:4], x[4:1], x[1:5], x[5:]にadd.reduceを適用 >>> y array([ 6, 4, 3, 7])しかしいったい何に使えるのだろうか。
サイズの異なる配列同士の演算は以下のルールに従って自動的に同じサイズの配列に変換して行われる。
- 出力される次元は入力配列の次元の最大のものになる
- 出力される各次元の要素数は入力される配列の要素数の最大のものになる。
- 入力される配列の次元のうち要素数が1かNoneの次元を出力次元になるように拡張(ブロードキャスト)する
- 1かNoneの次元がなければrank missmachでエラーになる。つまり入力配列は各次元で要素数が等しいか1かNoneでなければならない。
- 例1
>>> x = np . arange (4) >>> x = array ([0, 1, 2, 3]) >>> x + 3 array ([3, 4, 5, 6])
- 例2
>>> a = np.arange(12).reshape((3,4)) #次元(3,4)
>>> b = np.array([1,2,3])[:,np.newaxis] #次元(3,) np.newaxisは要素Noneの次元を後ろに追加する
>>> a + b
array([[ 1, 2, 3, 4],
[ 6, 7, 8, 9],
[11, 12, 13, 14]])
- 例3
>>> a = np.zeros((3,5)) #次元(3,5) >>> b = np.zeros(8) #次元(8) >>> c = a[...,np.newaxis] + b #...はEllipsisといい次元の数だけ:を展開する。この場合はa[:,:,np.newaxis] >>> c.shape #第1項は(3,5,)でbは(8)なので(3,5,8)にブロードキャストされる (3, 5, 8)
Pythonのリストと同じ。スライスは各次元で指定する必要があり指定がない次元は:が補完される。
- 例
>>> x = np.array([[[1],[2],[3]], [[4],[5],[6]]])
>>> x[:] #x[:,:,:]を表す。
array([[[1],
[2],
[3]],
[[4],
[5],
[6]]])
>>> x[1:2] #x[1:2,:,:]を表す。
array([[[4],
[5],
[6]]])
>>> x[:,1:2] #x[:,1:2,:]を表す。
>>> x[...,0] #x[:,:,0]を表す。
>>> x = np.arange(10)
>>> x[[0,2,2,4]] #np.array([x[0],x[2],x[2],x[4]])と等価
array([0, 2, 2, 4])
>>> x[np.array([[1,2],[3,1]])] #np.array([[x[1],x[2]],[x[3],x[1]]])と等価
array([[1, 2],
[3, 1]])
多次元配列でも同じ。ブロードキャストも有効。>>> x = np.ones(4) >>> x[np.array([1,2,3]),np.array([2,3,3])] #np.array([x[1,2],x[2,3],x[3,3]])と等価 array([ 0., 0., 1.])
bool型配列でmask。条件を満たす配列をスライスできる。
>>> x = np.arange(-5,5) >>> maxk = x > 0 >>> mask array([False, False, False, False, False, False, False, False, False, False], dtype=bool) >>> x[mask] array([1,2,3,4]) >>> x[x>0] array([1,2,3,4])条件が複数ある場合はビット演算子を使う。
>>> x[(x>0) & (x<2)] array([1]) >>> x[(x>0) | (x<0)] array([-5, -4, -3, -2, -1, 1, 2, 3, 4])論理型配列とnp.ndarrayクラスのany()、all()、where()メソッドを使うと様々なことができる。
>>> a>1
array([[False, False],
[ True, True]], dtype=bool)
>>> np.any(a>1) #bool型配列a>1の要素にTrueが一つでも含まれればTrue
True
>>> np.all(a>1) #a>1の要素がすべてTrueならTrue
False
これをブロードキャストと応用すると以下のようなこともできる。
>>> np.any(a>1,axis=1) #1軸(列)に沿って、つまり行を潰すように
array([ False, True], dtype=bool)
>>> a[np.any(a>1,axis=1),:] #1より大きい要素をもつ行を取り出す
array([[2, 3]])
>>> a[:,np.any(a>1,axis=0)] #1より大きい要素をもつ列を取り出す
array([[1],
[3]])
| max(a) | 最大値 |
|---|---|
| min(a) | 最小値 |
| nanmax/nanmin | NaNを無視して最大/最小値を検索 |
| argmax(a) | 最大値の要素のうち最も小さいインデックス |
| argmin(a) | 最小値の要素のうち最も小さいインデックス |
| nanargmax/nanargmin | NaNを無視したインデックスの検索 |
| where | 条件を満たす要素 |
| argwhere | 条件を満たす要素のインデックス |
| nonzero | ゼロでない要素のインデックス |
多次元配列の最大値/最小値の場所(インデックス)は1次元にしたときのインデックスで求まる。多次元配列の状態でのインデックスを求めたい場合は次のようにする。
>>> a = array([[10,50,30],[60,20,40]]) >>> a.argmax() 3 >>> np.unravel_index(a.argmax(), a.shape) (1, 0)
#緯度・経度のインデックス t_lon = int(np.where(lon==90)[0]) **カウント *masked array **作成 =|PY| #numpy ndarrayから x = np.array([1, 3, 4]) a = np.ma.array(x)

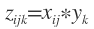
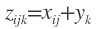

最新コメント