現在地：トップページ > ポリオミノの分類 > ポリオミノ：2ピース引き算の増殖形
概要
例
図で、1, 2, 3, 4, ...と、いくらでも大きい表現が存在する。
それぞれ第1段階、第2段階、…と呼ぶことが自然である。最初の図形を第0段階の図形とみなす。
議論
AB系列
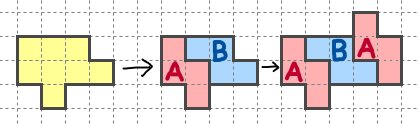
まず、前提として、ポリオミノを点対称な２つの図形（A+B）に分割できる時、もう一つAをつなげて全体を点対称にできる場合がある（重なる場合は例外）。
これは、文字列として捉えるのが分かりやすいだろう。「ABA」という文字列は回文になっている（回文というのはどちらかというと線対称に近いイメージだが、そこまで考えなくて良い）。
この考え方で行くと、「ABABA」や「ABABABA」なども、（回文であるため）、点対称になると予想される。すなわち、Aから始まる、AB交互の文字列で、長さが奇数のものは点対称になる。
しかも、最初の2文字を取り除いた文字列も、同じ条件を満たしている（長さが3以上の場合）。したがって、これは引き算の系列を作る。
この考え方を単純に式で表現するなら、
AB = (AB)A - A
AB = (AB)ABA - ABA
AB = (AB)ABABA - ABABA
...
といったところだろう。
この拡張は、Bが非連結なポリオミノであっても良い。重要なことは、AをBに対して対称移動させた図形が元のA自身と重ならないことである。
ここまで、個人的にAB系列と呼んでいる系列を説明した。
AC系列
P系列
Abq構成
引き算後が非連結なポリオミノだが、このような型があった。
青が対象の図形であり、点対称図形Aと、図形のペアb+qから構成される。これに点対称形であるA+Aを足すと、全体が点対称になる。しかし、A+Aは連結図形ではないため、(連結)-(連結)としての解にはならない。しかし(Abq, AA)のペアをAC型とみなすことができて、増殖することができる。増殖していくと、AC系列の意味での第2段階で初めて、(連結)-(連結)の表現になる。
AC系列はAB系列と比べて見つけにくい難点があるが、Abq構成ならば比較的見つけやすいと言えるだろう。
同形反復
ほとんど自明であるため言及することを忘れていたが、点対称形に対しては同形を反復する解が存在する。
同形反復の構成は、「n個の形」と「n+k個の形」の差分を取っている点が特徴である。kとして、1よりも大きい整数を考えることができる点にも注意する。
同形反復：はみ出し・切り取り
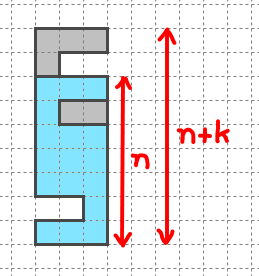
この構成を考える。
S字型の形は一般に中央の部分を「伸ばす」ことができる。伸ばしたものの差分を考えることで引き算の形ができて、これはnを任意に大きい整数にとれるため、増殖形になる。
この形は、よくよく見てみると同形反復とかなり類似している。実は、同形反復に枝をつけたものと解釈できる。
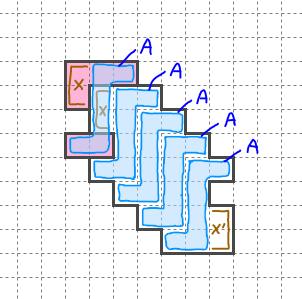
もう少し簡単と思われる例から考える。この形は、点対称な図形Aを同形反復した形をベースとして、Xで示している２か所の、「はみ出し」と「切り取り」を作っている形である。
この図が理解できれば、ある程度計画的に増殖形を生産することができる。
上の図は増殖する解を見つける際にも重要な着想を与える。すなわち、図形が与えられたとき、その一部分を併進してやることによって全体が点対称になるならば、増殖する解の系列が作れるのではないか？と予想することができる。
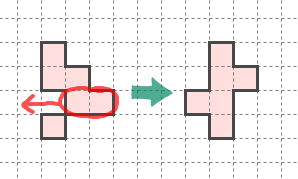
実際上のように点対称化できる形に対して、
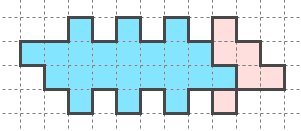
このように増殖解が存在している。
これはかなり面白い構成/解発見の仕方だと思えるのだが、残念ながら、併進で点対称になることは、十分条件ではない。
同形反復：幻の構成
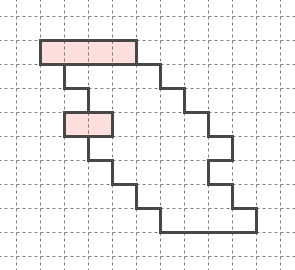
この増殖解は先ほどの「もう少し簡単と思われる例」を少し改変したもの。少し難しくなった。
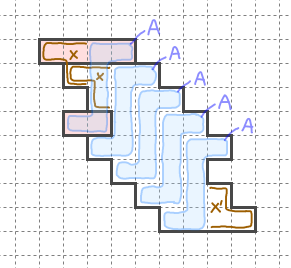
このように、「はみ出し」のXと「切り取り」のXが重なっている。
先ほどまでは、「切り取り」として、ベースとなるk図形（n+k図形からn図形を除いた形）の内部に納まる形を考えていたが、実は、「はみ出し」と重なる範囲であれば、k図形に納まらなくても良いのである。
このような増殖形を作る過程を、あえて解釈しようとするなら、
1. まず「幻のマス」をk図形に付加する（幻のマスは複数あっても良い）。
2. そのあとで、幻のマスを含む図形を併進する。
3. 最後に、本来存在しない幻のマス（併進前の位置のマス）を除去する。
といったところだろうか。
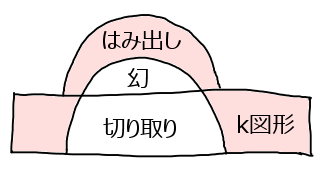
イメージ図で描くとこういった風になる。
上はあくまでイメージ図であるため正確性を欠いている可能性に注意が必要だが、この図から気づくことがある。
それは、図形が、どの位置で見ても一定の幅（高さ）を保っていることである。したがって、場所に依存する併進をすることで元のk図形を復元することができる。
一般には増殖の方向が斜めであるため、少しわかりにくいが、この法則が成り立つことが確認できる。
つまり、この変形は面積を保つ変形であり、増殖方向と垂直な方向の軸の値に依存する定数量だけ併進するものである。
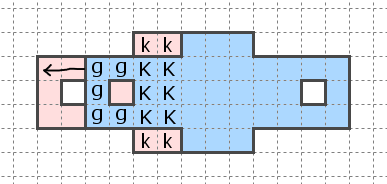
厳密には、この赤図形のように、複数回の併進に分けないと説明できない場合がある。ここで、kとKはベースとなるk図形、gは幻のを表す。
重なり増殖形
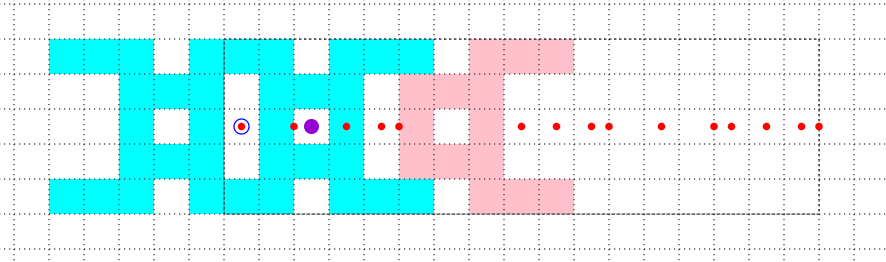
Tatt氏のツール（https://tatt61880.github.io/symmetry-mino-subtract...）を用いて増殖形を調べていた際に偶然見つけた形。
二つの増殖系列が同じ直線上に並んでいる。それだけなら驚かないが、周期が1.5の系列と周期が2の系列が並んでいる。このために、一見して不等間隔に点が配列している。
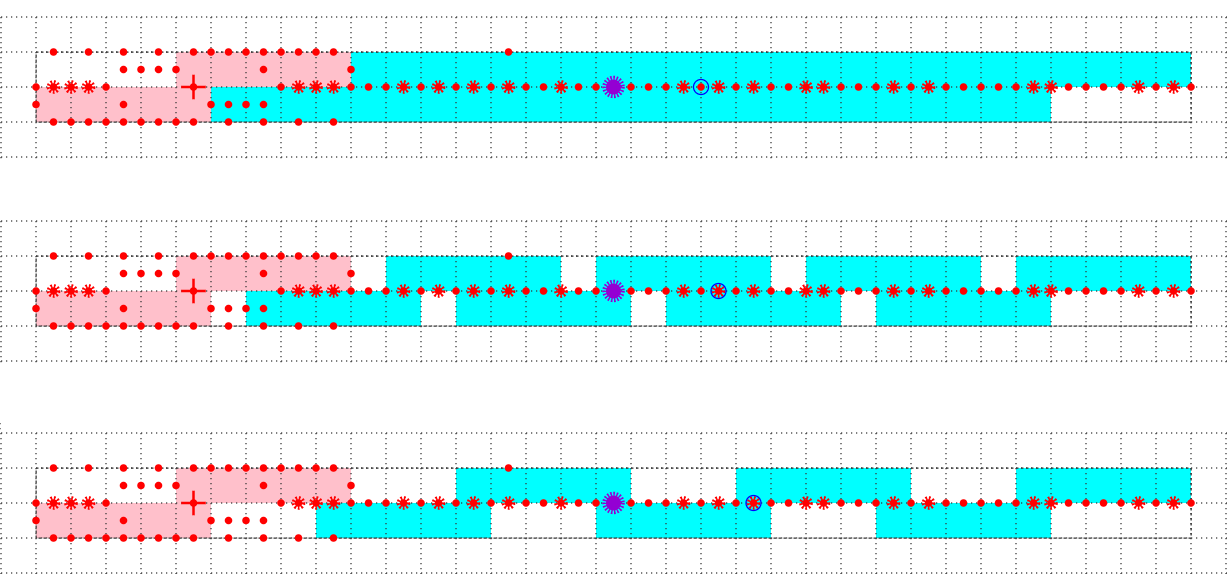
Tatt氏より。
ひとつ前のパターンは少しわかりにくかったが、Tatt氏の画像はいい具合に問題を単純化できている。これによって、複数の周期が生じる原因がいくらかわかるようになった。
概要 
例
図で、1, 2, 3, 4, ...と、いくらでも大きい表現が存在する。
それぞれ第1段階、第2段階、…と呼ぶことが自然である。最初の図形を第0段階の図形とみなす。
議論
AB系列
まず、前提として、ポリオミノを点対称な２つの図形（A+B）に分割できる時、もう一つAをつなげて全体を点対称にできる場合がある（重なる場合は例外）。
これは、文字列として捉えるのが分かりやすいだろう。「ABA」という文字列は回文になっている（回文というのはどちらかというと線対称に近いイメージだが、そこまで考えなくて良い）。
この考え方で行くと、「ABABA」や「ABABABA」なども、（回文であるため）、点対称になると予想される。すなわち、Aから始まる、AB交互の文字列で、長さが奇数のものは点対称になる。
しかも、最初の2文字を取り除いた文字列も、同じ条件を満たしている（長さが3以上の場合）。したがって、これは引き算の系列を作る。
この考え方を単純に式で表現するなら、
AB = (AB)A - A
AB = (AB)ABA - ABA
AB = (AB)ABABA - ABABA
...
といったところだろう。
この拡張は、Bが非連結なポリオミノであっても良い。重要なことは、AをBに対して対称移動させた図形が元のA自身と重ならないことである。
ここまで、個人的にAB系列と呼んでいる系列を説明した。
AC系列
次にAC系列を説明する。
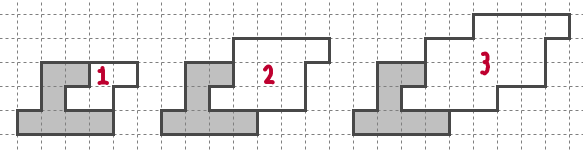
この形のことはまだ十分に理解ができていないが、私なりの説明を書く。
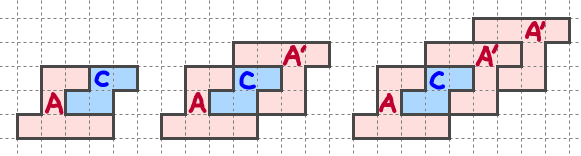
上図にA, Cと、Aの右肩にプライム記号を付けたA'の3つの記号を書いている。
AB型とは異なり、AとA'は点対称図形ではないことに注意する。Cは点対称である。
AとCをこの順番で連結した図形が点対称であることに注意する。ここで、
AC = CA'
が成立する。AとCの間に、ある種の交換関係が成り立っている、と思えば良いだろう。
Aに対して、まず最初にCを連結して、その後、繰り返しA'を連結していく図形を考えると、
AC = (点対称) （∵定義より）
ACA' = (点対称） （∵定義より）
ACA'A' = A(AC)A' = (点対称）
ACA'A'A' = AACA'A' = (点対称)
...
という風に、系列の全てが点対称になることがわかる。
AC系列に関しても、作成の際には、AをCに対して対称移動させたA'がAと重ならない、という点に気を付ける必要がある。
これは、例えば、AがCを「包み込む」ような形になっているような場合等に起こりうる。
AC系列を作ろう、という場合には、「AB系列で説明できる形になってしまわない」ということも要求したい場合がある。そのためには、Cが、「AC」図形の「半分を超える」ような構成にすると良いだろう。
上の2つの制約を同時に満たそうとした際には、増殖形の「すでに増殖している形」ができてしまうことが多い。それをしないために、追加の制約、すなわち、Aを「AC」図形内部で反転した際にA自身と重なる、という条件が求められる。
AC系列を作る方針を整理する。
1. 点対称な連結図形ACを作り、その図形を、点対称でない連結図形Aと、点対称な連結図形Cに分割する。 → （第一段階の）引き算表現が存在する。
2. AがCを「包み込む」ような形にならないようにする。 → AをCに対して対称移動した際に、A自身と重ならない。
3. Cが図形ACの「半分を超える」ようにする。 → Cを図形ACに対して対称移動した際に、C自身と重なる。
4. Aが図形ACの「半分を超える」ようにする。 → Aを図形ACに対して対称移動した際に、A自身と重なる。
上の方針の3と4は、一見して、矛盾している。しかし「半分を超える」という部分は、点対称移動した際に自身と重なる、ということなので、実は両方同時に満たすことができるのである。
実際に、上で例として載せていた構成はこの4つの条件を満たしている。
今後、上の4つの条件のそれぞれに関して個別に議論を行いたいため、4条件に名前を付けておく。
1. 第1減算条件
2. 作用点自立条件
3. 支点支配条件
4. 力点支配条件
なお、AB系列に関しても、上の「1. 第1減算条件」と「2. 作用点自立条件」と同じ条件が要求されるため、適宜同じ用語を用いる予定である。
ただしAB系列の場合は、第0段階の図形がABであることに注意する（AC系列では、第0段階の図形がAである）。段階一つあたりの増え方も異なることに注意する。
この形のことはまだ十分に理解ができていないが、私なりの説明を書く。
上図にA, Cと、Aの右肩にプライム記号を付けたA'の3つの記号を書いている。
AB型とは異なり、AとA'は点対称図形ではないことに注意する。Cは点対称である。
AとCをこの順番で連結した図形が点対称であることに注意する。ここで、
AC = CA'
が成立する。AとCの間に、ある種の交換関係が成り立っている、と思えば良いだろう。
Aに対して、まず最初にCを連結して、その後、繰り返しA'を連結していく図形を考えると、
AC = (点対称) （∵定義より）
ACA' = (点対称） （∵定義より）
ACA'A' = A(AC)A' = (点対称）
ACA'A'A' = AACA'A' = (点対称)
...
という風に、系列の全てが点対称になることがわかる。
AC系列に関しても、作成の際には、AをCに対して対称移動させたA'がAと重ならない、という点に気を付ける必要がある。
これは、例えば、AがCを「包み込む」ような形になっているような場合等に起こりうる。
AC系列を作ろう、という場合には、「AB系列で説明できる形になってしまわない」ということも要求したい場合がある。そのためには、Cが、「AC」図形の「半分を超える」ような構成にすると良いだろう。
上の2つの制約を同時に満たそうとした際には、増殖形の「すでに増殖している形」ができてしまうことが多い。それをしないために、追加の制約、すなわち、Aを「AC」図形内部で反転した際にA自身と重なる、という条件が求められる。
AC系列を作る方針を整理する。
1. 点対称な連結図形ACを作り、その図形を、点対称でない連結図形Aと、点対称な連結図形Cに分割する。 → （第一段階の）引き算表現が存在する。
2. AがCを「包み込む」ような形にならないようにする。 → AをCに対して対称移動した際に、A自身と重ならない。
3. Cが図形ACの「半分を超える」ようにする。 → Cを図形ACに対して対称移動した際に、C自身と重なる。
4. Aが図形ACの「半分を超える」ようにする。 → Aを図形ACに対して対称移動した際に、A自身と重なる。
上の方針の3と4は、一見して、矛盾している。しかし「半分を超える」という部分は、点対称移動した際に自身と重なる、ということなので、実は両方同時に満たすことができるのである。
実際に、上で例として載せていた構成はこの4つの条件を満たしている。
今後、上の4つの条件のそれぞれに関して個別に議論を行いたいため、4条件に名前を付けておく。
1. 第1減算条件
2. 作用点自立条件
3. 支点支配条件
4. 力点支配条件
なお、AB系列に関しても、上の「1. 第1減算条件」と「2. 作用点自立条件」と同じ条件が要求されるため、適宜同じ用語を用いる予定である。
ただしAB系列の場合は、第0段階の図形がABであることに注意する（AC系列では、第0段階の図形がAである）。段階一つあたりの増え方も異なることに注意する。
P系列
少し毛色が異なるが、まだ、特徴的な増殖形が存在する。それは、点対称な図形を、「穴の開いた点対称図形」で包んでいくような系列である。
これに関してはさほど面白くないため省略する。
これに関してはさほど面白くないため省略する。
Abq構成
引き算後が非連結なポリオミノだが、このような型があった。
青が対象の図形であり、点対称図形Aと、図形のペアb+qから構成される。これに点対称形であるA+Aを足すと、全体が点対称になる。しかし、A+Aは連結図形ではないため、(連結)-(連結)としての解にはならない。しかし(Abq, AA)のペアをAC型とみなすことができて、増殖することができる。増殖していくと、AC系列の意味での第2段階で初めて、(連結)-(連結)の表現になる。
AC系列はAB系列と比べて見つけにくい難点があるが、Abq構成ならば比較的見つけやすいと言えるだろう。
同形反復
ほとんど自明であるため言及することを忘れていたが、点対称形に対しては同形を反復する解が存在する。
同形反復の構成は、「n個の形」と「n+k個の形」の差分を取っている点が特徴である。kとして、1よりも大きい整数を考えることができる点にも注意する。
同形反復：はみ出し・切り取り
この構成を考える。
S字型の形は一般に中央の部分を「伸ばす」ことができる。伸ばしたものの差分を考えることで引き算の形ができて、これはnを任意に大きい整数にとれるため、増殖形になる。
この形は、よくよく見てみると同形反復とかなり類似している。実は、同形反復に枝をつけたものと解釈できる。
もう少し簡単と思われる例から考える。この形は、点対称な図形Aを同形反復した形をベースとして、Xで示している２か所の、「はみ出し」と「切り取り」を作っている形である。
この図が理解できれば、ある程度計画的に増殖形を生産することができる。
上の図は増殖する解を見つける際にも重要な着想を与える。すなわち、図形が与えられたとき、その一部分を併進してやることによって全体が点対称になるならば、増殖する解の系列が作れるのではないか？と予想することができる。
実際上のように点対称化できる形に対して、
このように増殖解が存在している。
これはかなり面白い構成/解発見の仕方だと思えるのだが、残念ながら、併進で点対称になることは、十分条件ではない。
同形反復：幻の構成
この増殖解は先ほどの「もう少し簡単と思われる例」を少し改変したもの。少し難しくなった。
このように、「はみ出し」のXと「切り取り」のXが重なっている。
先ほどまでは、「切り取り」として、ベースとなるk図形（n+k図形からn図形を除いた形）の内部に納まる形を考えていたが、実は、「はみ出し」と重なる範囲であれば、k図形に納まらなくても良いのである。
このような増殖形を作る過程を、あえて解釈しようとするなら、
1. まず「幻のマス」をk図形に付加する（幻のマスは複数あっても良い）。
2. そのあとで、幻のマスを含む図形を併進する。
3. 最後に、本来存在しない幻のマス（併進前の位置のマス）を除去する。
といったところだろうか。
イメージ図で描くとこういった風になる。
上はあくまでイメージ図であるため正確性を欠いている可能性に注意が必要だが、この図から気づくことがある。
それは、図形が、どの位置で見ても一定の幅（高さ）を保っていることである。したがって、場所に依存する併進をすることで元のk図形を復元することができる。
一般には増殖の方向が斜めであるため、少しわかりにくいが、この法則が成り立つことが確認できる。
つまり、この変形は面積を保つ変形であり、増殖方向と垂直な方向の軸の値に依存する定数量だけ併進するものである。
厳密には、この赤図形のように、複数回の併進に分けないと説明できない場合がある。ここで、kとKはベースとなるk図形、gは幻のを表す。
重なり増殖形
Tatt氏のツール（https://tatt61880.github.io/symmetry-mino-subtract...）を用いて増殖形を調べていた際に偶然見つけた形。
二つの増殖系列が同じ直線上に並んでいる。それだけなら驚かないが、周期が1.5の系列と周期が2の系列が並んでいる。このために、一見して不等間隔に点が配列している。
Tatt氏より。
ひとつ前のパターンは少しわかりにくかったが、Tatt氏の画像はいい具合に問題を単純化できている。これによって、複数の周期が生じる原因がいくらかわかるようになった。
コメントをかく