天体ショー研究Wiki

なぞれ！ポリオミノ|うまや天国|note

穴の空いていない、また、頂点接触のない、ポリオミノを想定する（今はエッジだけに興味があるため）。
点対称の場合、凹みは偶数個存在するため、凹凸列の長さが偶数になる。しかも、その二つの凹みの間の時計回りの経路２つにおいて、凹と凸の並び方は同一になるはずであるため、凹凸列は同じ数列を2回繰り返したものになる。

ある凹凸列について、その凹凸列を凹凸列表現の集合に持つ点対称図形が存在する時、その凹凸列は点対称であると言うことにする。


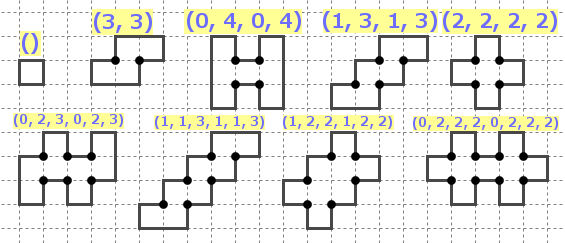
サイズ9までの点対称単連結ポリオミノについて、凹凸列は上の9通り。

ここで、凹凸列の基本的な性質について調べておく。

任意の（単連結、頂点接触なし）ポリオミノについて、隣り合う頂点が凹+凸である時、その2つのペアを同時に消したような凹凸の列のポリオミノが存在する（消すような変形が存在する）。ポリオミノに凹と凸の両方の頂点が存在するならば、凹と凸が隣り合っている箇所が少なくとも一か所必ず存在するため、この変形を繰り返し適用することができる。最終的に凸だけまたは凹だけのポリオミノとなるが、ポリオミノは多角形であるため、内部の角度の和が外部の角度の和を超えることはない。したがって最終的には凸だけになるが、そのような図形は長方形だけである。長方形は凸が4つあるため、帰納法から凸は凹よりちょうど4つ多いことがわかる。
点対称図形の場合は凹頂点が偶数個2n個あるため、凸頂点は2n+4個ある。凹凸列は凸な頂点を凹な頂点で分割する方法を与えるものである。すなわち、2n+4を2n個に分割する数列である。
次に凹凸列の変形について考える。
ある凹頂点に注目する、隣に凸頂点が存在するとすると、凹頂点と凸頂点を交換するような変形が可能である。これを実行すると、凹凸列における数の分割位置がひとつずれる。つまり、
(a_1, a_2, ... a_k, a_{k+1}, ... a_2n) → (a_1, a_2, ... a_k-1, a_{k+1}+1, ... a_2n)
と変形できる（a_k≠0の場合）。これは、凹凸列内で自由に数を移動していくことができることを意味している。したがって、任意の数の配置が可能である。

凹凸列は2n+4を2n個の非負整数に分割する方法である。nが大きいとき、2n+4と2nは同じスケールとなるため、感覚としては、大部分が0〜2になる（平均が1になる）分布が期待される。逆に大きい数を作ろうとすると、0がたくさん存在する領域を作らないといけない。そうすると「豚のしっぽ」のように空間をぐるぐると閉じ込める形ができやすい、と考えられる。