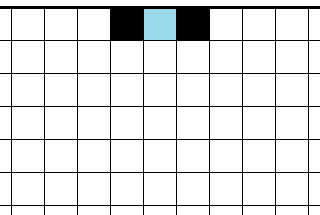
�䥸���μ�ڽ��Ǥ���
���ա�
�ѥ���ˤϼ�ʬ�DzƼ�ʬ�Ǽ�ڤĤ��Ƥ����Ȥ����ڤ������⤢��ޤ���
���μ�ڽ��Ϥ���Х䥸���ι�ά����ڡ����Τ褦�ʤ�ΤʤΤǡ�����Ȥ��ˤϤ��Τ��Ȥ�α�դ��Ƥ��������͡�
���Τ褦�˥ޥ����濴���̤�褦�˰����ޤ���
�롼�����顢���ϸ�ʬ�������뤳�Ȥʤ����ǽ�Ū���������Ĥ��ؤä��ʥ롼�סˤˤʤ�褦�ˤ��ޤ���
���Υ롼�뤫���äˤ���ޥ��������̤��硢ɬ�������դ������ꤢ���դ���Ф뤳�Ȥˤʤ�ޤ���
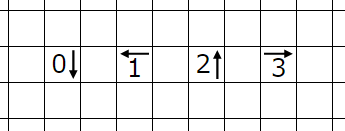
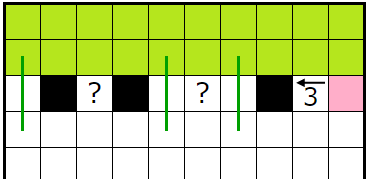
��:��������
���������ҥ�Ȥ�ͤ��ޤ���
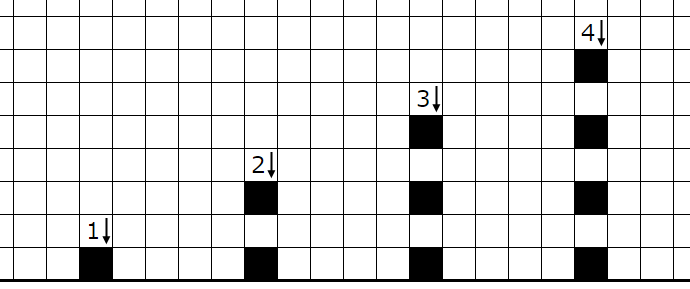
�ؤ��Ƥ��������Υޥ��ο��ܹ��ޥ��ϥ��ƥ襳��Ϣ³���ʤ��Ȥ����롼�뤫����ޥ������Τ褦�˳��ꤷ�ޤ���
���ʤߤ����Ϥ��Τ褦�˳��ꤷ�ޤ��ʼ��ϡ��ؤ��Ƥ�������˥ҥ�Ȥ�̵������
1��2n-1�ޥ�����ʬ��������ޥ��Ŀ���¤�n�Ĥ������������̤ꤷ���ʤ����ᡢ������ʬ��n�Ĺ��ޥ�������ȸ���줿�����ꤷ�ޤ���
������������Ȥ˸����äƤȤ������ϤȤƤ�褯�Ф�Τǡ�������γ���ѥ��������dzФ�������褦�ˤʤ뤫�⤷��ޤ���
�������Τǣ��ĤΥ롼�פˤʤ�ʤ���Фʤ�ʤ��Ȥ����롼��ˤʤäƤ���Τǡ�¾�������ڤ�ü������/���ޥ������Ǥ������ʤ�����ޥ����������������ʬŪ�˥롼�פ��äƤϤ����ʤ��Ȥ�����ڤǤ���
��
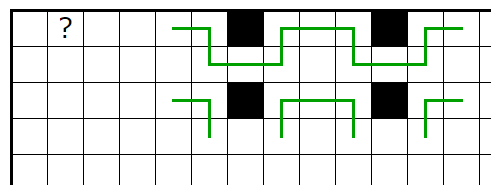
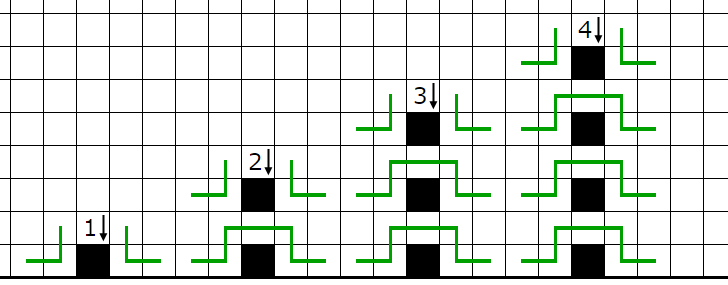
���Τ褦�ʾ��������ä��Ȥ��ޤ���

��������ü�ϱ��˹Ԥ�����ʬŪ�˥롼�פ�����Ƥ��ޤ������˹Ԥ���������ޤ���

����˾��롼�ؤμ�ڤ��Ѥ��Ƴ��ꤹ������ü�����Ф����ޤǤ���
���롼�פ�����ʤ��褦������ü�Ф��ƹԤ��Ⱥǽ�Ū�ˤ����ޤdz��ꤹ�뤳�Ȥ�����ޤ���
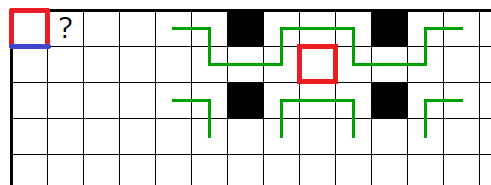
������ʬ��������ޥ��ο��ξ�¤�ͤ��뤳�Ȥǹ��ޥ������ꤹ���礬����ޤ���
�����Ǥϥҥ�Ȥλؤ��Ƥ��룱��ʹԡˤζ���ޥ������������ޥ�����ͤ��ޤ���
��2n�ޥ��ζ���ޥ��ˤϡ�n��
��2n-1�ޥ��ζ���ޥ��ˤ�n��
�ι��ޥ�������뤳�Ȥ��Ǥ��ޤ����ä�2n-1�ޥ��ζ���ޥ���n�Ĺ��ޥ��������Ȥ����������ϡ�1�����Ф��ι��פμ�������Ǹ����̤������������ꤷ�ޤ���
����ˤ�äƻؤ��Ƥ��������ζ���ޥ��ζ��ڤ����+�ҥ�Ȥι��ޥ����ˤ�äƤϹ��ޥ��ΰ��֤���ʬŪ�˳��ꤹ�뤳�Ȥ�����ޤ���
��
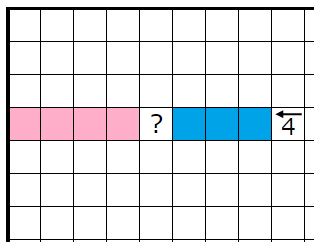
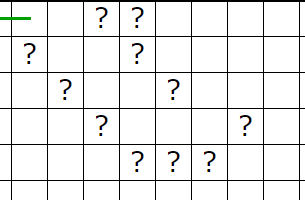
�ԥ�����ʬ�ˤϹ��ޥ������磲�ġ��ĥޥ�����ʬ�ˤϹ��ޥ������磲��������ޤ����ҥ�Ȥ����ʤΤǤ��줾�죲�Ĥ��Ĺ��ޥ�������ʤ���Фʤ�ʤ����Ȥ�ʬ����ޤ���
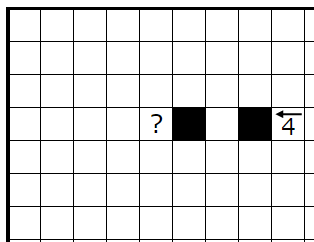
�Ŀ�����ʬ�ϡ�1�����Ф��ι��פ����ޥ�����ꤹ�뤳�Ȥ��Ǥ��ޤ���
����ޥ����������Ǥ���Ȥ����ޥ��Ȥ���ޤ��Ȥ��������ꤷ̷�⤹��Ȥ��β�ǽ����̵�����Ȥ�ʬ����ޤ���
2n-1�ζ�֤�n�Ĥι��ޥ�������Ȥ���ȡĤȤ���ñ�㲾�����ʬ����Ȥ��ˤ褯����ޤ���
�äˤ���ޥ�����ޥ��Ȳ��ꤷ��̷�⤷���餽�Υޥ�����ޥ�����ޥ��Ȳ��ꤷ��̷�⤷������ޥ��Ǥ���
�ʲ��������Ĥ������Ƥߤޤ���
������ǽƤ����ü��ˡ�פȤ�����ڤ�������ȯŸ����Ԥ˽Ƥ���ޤ���
���ޥ��Ǥ���Ȳ��ꤷ��̷�⤹���㭡�ʾ��롼�ء�
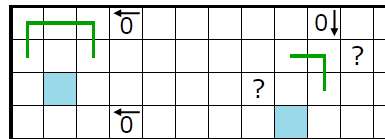
�忧�Υޥ��Ϲ��ޥ��Ȳ��ꤷ����������Ƥߤ�Ⱦ��롼�פ������̷�⤹��Τǡ���ޥ��Ǥ��뤳�Ȥ�ʬ����ޤ���
���ޥ��Ǥ���Ȳ��ꤷ��̷�⤹���㭢��ü��ˡ��

�忧�Υޥ��Ϲ��ޥ��Ȳ��ꤹ��Ⱥ������ʬ����������ü�ο�������ܤˤʤ뤿��̷�⡢��ä���ޥ���ͭ�뤳�Ȥ�ʬ����ޤ���
��ޤ��Ǥ���Ȳ��ꤷ��̷�⤹���㭡�ʾ��롼�ء�
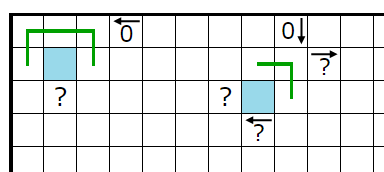
�忧�Υޥ�����ޥ��Ȳ��ꤷ����������Ƥߤ�Ⱦ��롼�פ������̷�⤹��Τǡ����ޥ��Ǥ��뤳�Ȥ�ʬ����ޤ���
��ޤ��Ǥ���Ȳ��ꤷ��̷�⤹���㭢��ü��ˡ��
�忧�Υޥ�����ޥ��Ȳ��ꤷ����������Ƥߤ�Ⱥ������ʬ����������ü�ο�������ܤˤʤ뤿��̷�⡢��äƹ��ޥ���ͭ�뤳�Ȥ�ʬ����ޤ���
���礦�ɣ������ɤ��äƤ���ޥ��ϡ����ܤ���ޥ��Τ����ɤ��äƤʤ������ˤ���ޥ�����ޥ��Ǥ��뤳�Ȥ�ʬ����ޤ���
���դ���ʬ����Ť餤�ΤǤ����㤨�о�ޤǡ����ǤäƤ���ޥ��������ǡ��º���ޥ��ˤʤ�ޤ���
��ͳ�Ϲ��ޥ���ñ�㲾�ꤷ�Ƥߤ��ʬ����ޤ������忧�Υޥ������̤줺�ι��פˤ����ޥ��ˤʤ�Τǹ��ޥ���Ϣ³����̷�⤹�뤫��Ǥ���
�äˡ�������֤����̤ˤ����ƳѤ��٤οޤǡ����ǤäƤ���ޥ��ϤϤ��ᤫ����ޥ��ʤΤ����ꤷ�Ƥ��ޤ���
���礦�ɣ������ɤ��äƤ���ޥ������ĥ��ƥ襳��Ϣ³���Ƥ���Ȥ��������Υޥ��������̤뤳�Ȥ�ʬ���ꡢ���������ΰ����������ꤷ�ޤ���
��
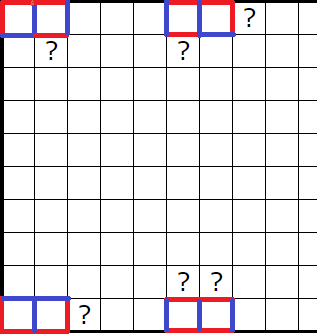
�㤨�о�������������ǰϤޤ줿��ʬ��ͤ��ޤ��������Ϻɤ��äƤ��������������Ϻɤ��äƤ��ʤ�������ɽ���Ƥ��ޤ���Ϣ³����ޥ��Τ��������ˡ�ñ�㲾��α��ѡʽи��������ˡפ�Ȥ��Ȥ⤦��������ޥ��Ǥ��뤳�Ȥ��狼�ꡢ�⤦�������Ф��ơ�ñ�㲾��α��ѡʽи��������ˡפ�Ȥ�����������ޥ��Ǥ��뤳�Ȥ�ʬ����ޤ���

��䤳���������ޤ���������������������ǰϤޤ줿�ޥ��Ϥɤ������ޥ��Ǥ��뤳�Ȥ����ꤹ��Ȥ������ȤǤ��������Ǥ��礦�ɣ������ɤ��äƤ���ޥ��Ǥ⤢�ä��Τǡ��������ꤷ�ޤ���
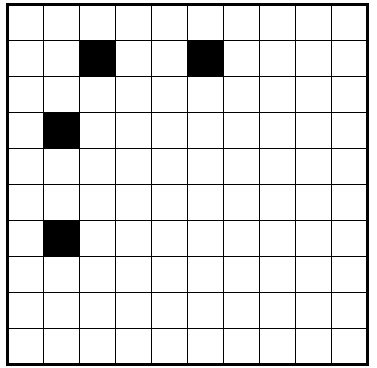
����ü���飲���ܤιԡ���ˤϡʤ��ιԡ���䤽�ζ������ü�ιԡ���˥ҥ�Ȥ�̵�����ˤϡˣ������Ф��ǤϹ��ޥ���������ޤ���äƹ��ޥ��������ʤ飲�����Ф��ʾ�ˤʤ�ޤ����ʡ��ɺ������פǡ��դ������פ�����Ƥ�����⤢��Τ��ʤȻפä��ΤǤ�������ͳ�Υ����å����㤦�����̤Τ�ΤȤ��ư����ޤ�������
��ͳ:
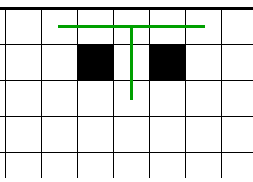
�ºݣ������Ф�������Ƥߤ�����λ���ϩ��ȯ�����Ƥ��ޤ�̷�⤹�뤫��Ǥ���
�����������ιԡ���䤽�ζ������ü�ιԡ���˥ҥ�Ȥ�̵����֤ξ�����äʤΤǡ����Τ褦�ʥҥ�Ȥ������磱�����Ф��Ǥ��֤��뤳�Ȥ⤢�뤳�Ȥ����դ��Ƥ���������
���ν����꤬����ʾ�Ǥ��ʤ����ڡ����������������ü�θĿ��϶����ܤǤʤ��Ȥ����ʤ��Ȥ���ˡ§�Ǥ���
������������Ȳ��ꤷ����硢�ɤΤ褦������ü�äĤ����Ȥ��Ƥ⣱������ü��;�äƤ��ޤ����Ȥ���ʬ����ޤ���
�ºݤλȤ����Ȥ��Ƥϡ����Σ�����Τ��������ä���Ф뤳�Ȥ��Ǥ�������Ǥ����������̤�뤫�����������Ϥɤ��ʤ뤫����ꤹ�뤳�Ȥ��Ǥ��ޤ���
����������ҤΡ�ñ�㲾��פι�ˤ⤢��ޤ����������Ǥ⣱�ľҲ𤷤����Ȼפ��ޤ���
��
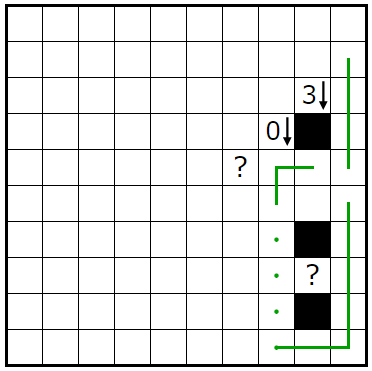
�㤨�Ф���ʾ������ä��Ȥ��ޤ���
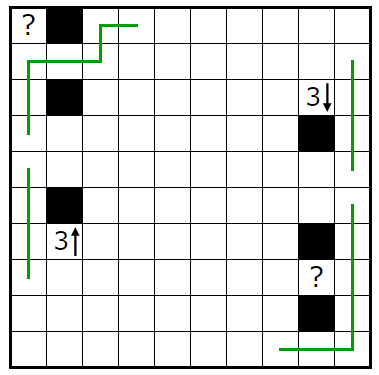
�ִݤ�����ü�ڤӲ��п��Υ��ڡ�����ͤ���ȡ����Ȳ��п��Υ��ڡ����˽�����Ǥ�������ü���ִݤΤߤǤ��������п��Υ��ڡ����ˤ�������ü���ܿ��ϣ��ܡʴ���ܡˤΰ٤��ȣ�������ü��������ޤʤ���̷�⤹�뤳�Ȥˤʤ�ޤ���
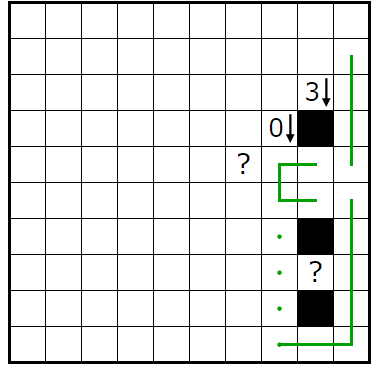
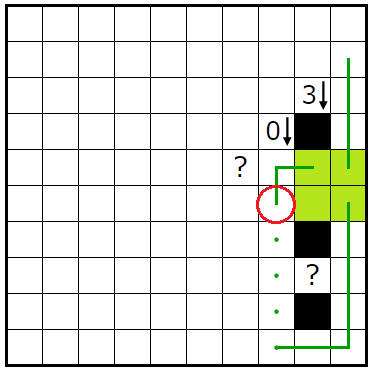
��ä��ִݤ�����ü�ϱ��˹Ԥ����Ȥ�ʬ����ޤ�����
ü��ˡ�ϱ����ϰϤ������Ǥ����������ǤϹ��ޥ�����ߤΣ����Ҳ𤷤ޤ���
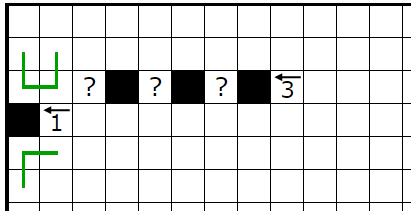
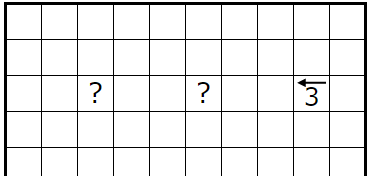
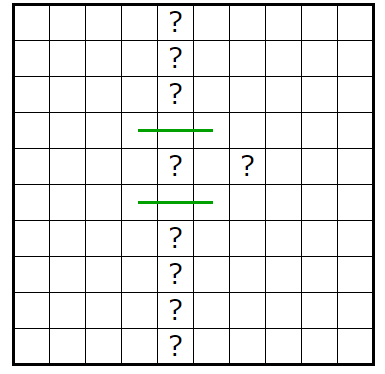
�㣱

��������������ͤ��ޤ��������Ǥϣ�����ͤ��ޤ���
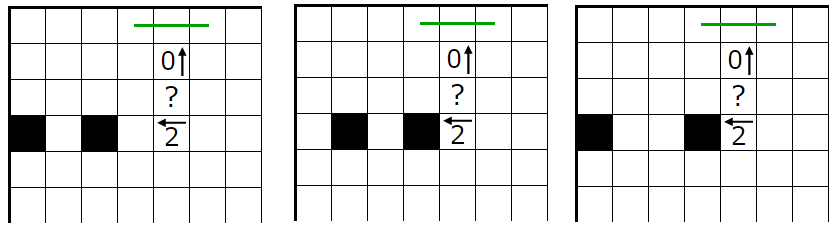
�����Υҥ�Ȥ��������ϣ��̤ꤢ��ޤ�����
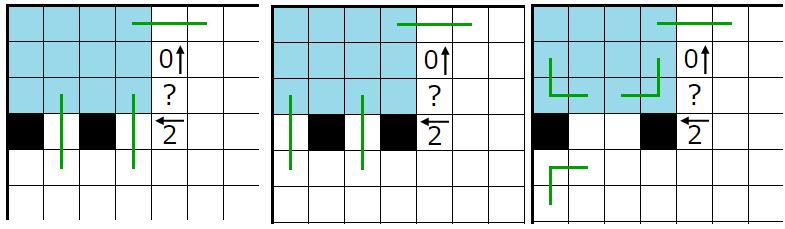
���Σ���˴ؤ��ƿ忧����ʬ��ͤ��Ƥߤ�ȡ����ν�����Ϥ⤦�Ǥ��ޤ�������ü������ܡʣ��ܡˤˤʤäƤ���Τ�̷�⡣
��äƣ����Υҥ�Ȥǹͤ�������ޥ����������Σ��̤��棲�̤꤬������ä��ΤǻĤ���ޥ����������dz��ꤹ�뤳�Ȥˤʤ�ޤ���
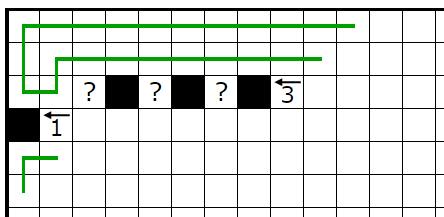
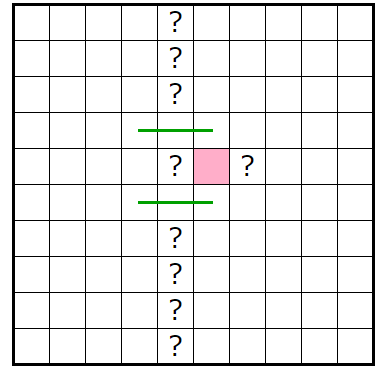
�㣲
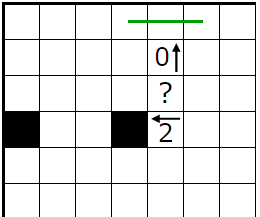
��������������ͤ��ޤ���
�����Υҥ�Ȥȡ��忧�γ�1��2����ʬ��������ޥ���¿����顢��1��2����ʬ�ˤϣ��Ĥ��Ĺ��ޥ������뤳�Ȥ�ʬ����ޤ���

��1��2�ޥ��Τɤ���˹��ޥ�������Ƥ⡢������ˤ�������п��ζ��֤ˤϳƣ��ܤ��ġ��ף��ܹ��ޥ���������ळ�Ȥ�ʬ����ޤ���
�ޤ�������п�����ʬ�Ǥ����������ꤳ��;�Ϥ�����Τϥԥ��Υޥ��ΤߤǤ��뤳�Ȥˤ����դ��ޤ���
��äơ��ԥ��Υޥ�����ޥ��Ȳ��ꤹ��ȡ�����п�����ʬ�������������ü�ϣ��ܡʴ���ܡˤȤʤä�̷�⤷�ޤ���

�ʾ���ԥ��Υޥ��Ϲ��ޥ��Ǥʤ��Τ������̤�ޥ��Ǥ��뤳�Ȥ�ʬ���ꡢ���Τ褦���������ꤷ�ޤ���
���롼�ؤ�¾�������ڤ�ü������/���ޥ������Ǥ������ʤ�����ޥ����������������ʬŪ�˥롼�פ��äƤϤ����ʤ��Ȥ�����ڤǤ����������ǤϾ��롼�ؤ��ͤ�����辮�롼�ؤ�������ޥ������Ǥ������ʤ����ڡ����ˤϡ����Υ��ڡ�������Ὢ���ޤdz�����������ꤹ������ü�����ʤ��Ȥ�2�ܤ�¸�ߤ��ʤ���Фʤ�ʤ��ʤǤʤ��ȳ���ʬ�ˤɤ����Ƥ⾮�롼�פ�������ˤ��Ȥ����ޤ��ڤΤ��ȤȤ��ޤ���
�狼��Ť餤�Τ����Ф��ޤ���
��

���Τ褦�ʾ�����ͤ��ޤ���
��¦����ʬ�⺸¦����ʬ����ޥ������Ǥ������ʤ��ΤǤ��Τ褦�������̤뤳�Ȥ�ʬ����ޤ���
�ޤ��ԥ��Υޥ�����ޥ��Ȳ��ꤷ����������ȡ���¦�Υ��ڡ����Ǥɤ��Ĥʤ��������롼�פˤʤ�Τǹ��ޥ��ˤʤ�ޤ���
�ޤ�������ʷ�ޤ����⤢��ޤ���

�ڥ�ѥ���Τ���«�Ȥ��Ƥ��������ͣ���Ǥ����ͣ���Ǥʤ��ʤ�����������Ǥ���ˤȤ����Τ�����ΤǤ����������ռ�ˤȤä����̤�ʤ餳��������ޤ����뤷���ʤ��������Ȥ���������Ǥ�����ڤȤ���������̯�Ǥ����ġ�
���ա�
�ֲ褦�˺��פȤ����褦�˺��������ͣ������Ȥäƹ��ޥ�����������Τϴ����Ǥ����ʤ��ʤ餽�Υѥ��뤬ͣ���Ǥ��롢�Ȥ������Ȥ�����Ȥ���������Τ��ᡢ��äƤ����ʳ���ͣ���ʬ����ʤ����֤ǤϻȤ��ʤ�����Ǥ���
������������줷���ʤ�����ѥ�����ˤʤ뤳�Ȥ⤢��ޤ����ġ�
�����ǤϺ����ˤ���ˤ�褯�ФƤ���ѥ������Ҳ𤷤ޤ���

����Ǥ���
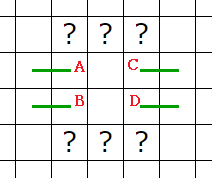
�������뤿�������ü�ˤ��줾������¡��á��ĤȤ���̾�����դ��ޤ���
���ȣ¡��äȣĤ�Ĥʤ��Ĥʤ����ϣ��̤ꤢ��Τ�����β�ͣ���ʤ���ȣ¡��äȣĤ�Ĥʤ����Ȥ�̵����ʬ����ޤ���

���ȣ¡��äȣĤ�Ĥʤ��ǤϤ����ʤ���ʬ����Ф��Τ褦�����������뤳�Ȥ�ʬ����ޤ���
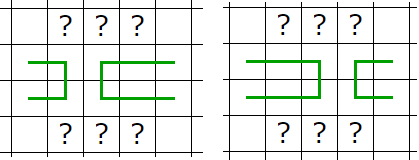
��������äƤ��Ƥ��Υѥ����Ф���ᤷ���ġ�
��äƤ���Ȥ��ˤ��Υѥ����Ф�ȳ������龮�롼�ؤǤ�����ʬ�����Ǥ���褦�ˤ��ʤ��Ȥ����ʤ��ΤǤȤƤⵤ���ޤ������⤦������ʬ��ä��ƿ����ͤ��ʤ������Ȥ������Ȥ�ͤ��ޤ���
�ޤ����֤Σ��ޥ���ҥ�Ȥ�����Ȥ���Ķ�ϵ��⤢��ޤ����ġ�
�Ǹ�μ��ʤǤ������ꤷ�����Τޤ���ǤⲾ�ꤷ�Ʋ��Ǥ��������Ȥ�ʤ���вʤ�����ϴ���Ū�ˤȤƤ����Ǥ���
��Х�������٤��ȤƤ�⤤��Х��䥸���λ��Ǥ����ͤˤ�äƤɤ������Х��Ȥ��뤫�Ͻ��⤢��ޤ��ˤϤ����Ȥ�ʤ��Ȳʤ����Ȥ�¿������ޤ���
�����ˤ�䥸���μ�ڤˤĤ��ƽƤ��뵭����ޤȤ¸�ߤ��ޤ��ΤǾҲ𤵤���ĺ���ޤ������Υڡ����˽Ƥ��ʤ���ڤ⤢��ޤ��Τ�����������������
��Х���ڽ�(�ʰ���)--SP1�ΤѤ���ˤä�
SP1��ˤ��䥸����ڽ��Ǥ�����Х��Ȥ���ޤ�������Х��䥸���Τ��ȤʤΤǥ䥸���Ǥ���
�䥸����ڤޤȤ�
�դ����ߤΤ���ˤ��䥸����ڽ��Ǥ���
���ա�
�ѥ���ˤϼ�ʬ�DzƼ�ʬ�Ǽ�ڤĤ��Ƥ����Ȥ����ڤ������⤢��ޤ���
���μ�ڽ��Ϥ���Х䥸���ι�ά����ڡ����Τ褦�ʤ�ΤʤΤǡ�����Ȥ��ˤϤ��Τ��Ȥ�α�դ��Ƥ��������͡�

���Τ褦�˥ޥ����濴���̤�褦�˰����ޤ���
�롼�����顢���ϸ�ʬ�������뤳�Ȥʤ����ǽ�Ū���������Ĥ��ؤä��ʥ롼�סˤˤʤ�褦�ˤ��ޤ���
���Υ롼�뤫���äˤ���ޥ��������̤��硢ɬ�������դ������ꤢ���դ���Ф뤳�Ȥˤʤ�ޤ���
��ޥ��������̤�ȳ��ꤷ���ޥ��ˤΤ��������礦�ɣ��դ��ɤ��äƤ����Τ������̤��������ꤹ�뤿�����������ޤ���
���դ�������ʬ����Ť餤�ΤǶ������������������
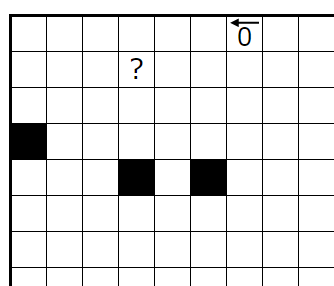
�����������������ä��Ȥ��ޤ���
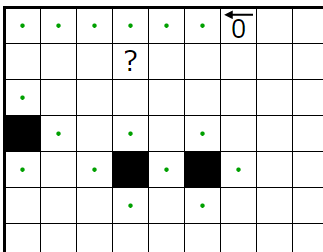
�����ΰ٤���ޥ������ꤹ��ޥ��ˡ����Ǥ��ޤ��������ޥ��ϥ��ƥ襳��Ϣ³���ƤϤ����ʤ��Ȥ����롼�뤫�顢���ޥ����٤Ϥʤ�餫����������ޥ�����ޥ��ˤˤʤ�ޤ���
�ޤ��������Υҥ�Ȥ����ޥ�������ʤ��Τǻؤ��Ƥ�����������ѥ�����ȤޤǤΥޥ�����������ޥ�����ޥ��ˤˤʤ�ޤ���
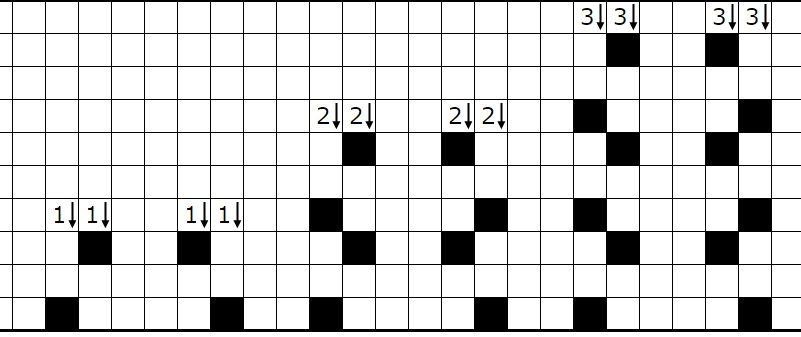
��β����������������ˤ��Ϥޤ�Ƥ���ޥ��ˤĤ��ƹͤ��ޤ������줾�������Ϻɤ��äƤ����ա������������Ф����դ�ɽ���ޤ��������Ф����դ����Ĥξ�硢���ΰ����������̤ꤷ���ʤ�������ꤷ�ޤ���
���ꤹ����������ޤ�����
���դ�������ʬ����Ť餤�ΤǶ������������������

�����������������ä��Ȥ��ޤ���

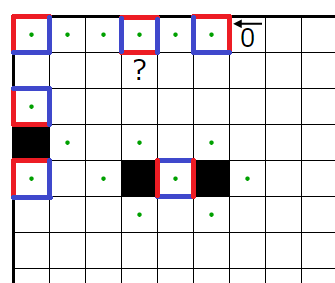
�����ΰ٤���ޥ������ꤹ��ޥ��ˡ����Ǥ��ޤ��������ޥ��ϥ��ƥ襳��Ϣ³���ƤϤ����ʤ��Ȥ����롼�뤫�顢���ޥ����٤Ϥʤ�餫����������ޥ�����ޥ��ˤˤʤ�ޤ���
�ޤ��������Υҥ�Ȥ����ޥ�������ʤ��Τǻؤ��Ƥ�����������ѥ�����ȤޤǤΥޥ�����������ޥ�����ޥ��ˤˤʤ�ޤ���

��β����������������ˤ��Ϥޤ�Ƥ���ޥ��ˤĤ��ƹͤ��ޤ������줾�������Ϻɤ��äƤ����ա������������Ф����դ�ɽ���ޤ��������Ф����դ����Ĥξ�硢���ΰ����������̤ꤷ���ʤ�������ꤷ�ޤ���

���ꤹ����������ޤ�����
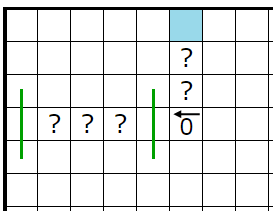
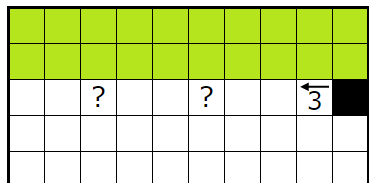
��:��������

���������ҥ�Ȥ�ͤ��ޤ���

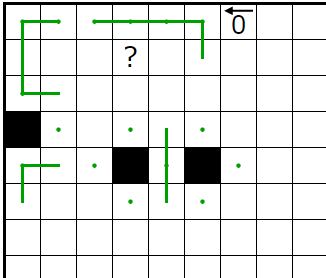
�ؤ��Ƥ��������Υޥ��ο��ܹ��ޥ��ϥ��ƥ襳��Ϣ³���ʤ��Ȥ����롼�뤫����ޥ������Τ褦�˳��ꤷ�ޤ���

���ʤߤ����Ϥ��Τ褦�˳��ꤷ�ޤ��ʼ��ϡ��ؤ��Ƥ�������˥ҥ�Ȥ�̵������
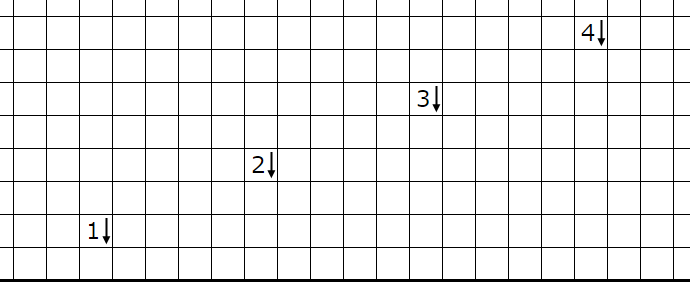
1��2n-1�ޥ�����ʬ��������ޥ��Ŀ���¤�n�Ĥ������������̤ꤷ���ʤ����ᡢ������ʬ��n�Ĺ��ޥ�������ȸ���줿�����ꤷ�ޤ���
������������Ȥ˸����äƤȤ������ϤȤƤ�褯�Ф�Τǡ�������γ���ѥ��������dzФ�������褦�ˤʤ뤫�⤷��ޤ���
�������Τǣ��ĤΥ롼�פˤʤ�ʤ���Фʤ�ʤ��Ȥ����롼��ˤʤäƤ���Τǡ�¾�������ڤ�ü������/���ޥ������Ǥ������ʤ�����ޥ����������������ʬŪ�˥롼�פ��äƤϤ����ʤ��Ȥ�����ڤǤ���
��

���Τ褦�ʾ��������ä��Ȥ��ޤ���

��������ü�ϱ��˹Ԥ�����ʬŪ�˥롼�פ�����Ƥ��ޤ������˹Ԥ���������ޤ���

����˾��롼�ؤμ�ڤ��Ѥ��Ƴ��ꤹ������ü�����Ф����ޤǤ���

���롼�פ�����ʤ��褦������ü�Ф��ƹԤ��Ⱥǽ�Ū�ˤ����ޤdz��ꤹ�뤳�Ȥ�����ޤ���
������ʬ��������ޥ��ο��ξ�¤�ͤ��뤳�Ȥǹ��ޥ������ꤹ���礬����ޤ���
�����Ǥϥҥ�Ȥλؤ��Ƥ��룱��ʹԡˤζ���ޥ������������ޥ�����ͤ��ޤ���
��2n�ޥ��ζ���ޥ��ˤϡ�n��
��2n-1�ޥ��ζ���ޥ��ˤ�n��
�ι��ޥ�������뤳�Ȥ��Ǥ��ޤ����ä�2n-1�ޥ��ζ���ޥ���n�Ĺ��ޥ��������Ȥ����������ϡ�1�����Ф��ι��פμ�������Ǹ����̤������������ꤷ�ޤ���
����ˤ�äƻؤ��Ƥ��������ζ���ޥ��ζ��ڤ����+�ҥ�Ȥι��ޥ����ˤ�äƤϹ��ޥ��ΰ��֤���ʬŪ�˳��ꤹ�뤳�Ȥ�����ޤ���
��

�ԥ�����ʬ�ˤϹ��ޥ������磲�ġ��ĥޥ�����ʬ�ˤϹ��ޥ������磲��������ޤ����ҥ�Ȥ����ʤΤǤ��줾�죲�Ĥ��Ĺ��ޥ�������ʤ���Фʤ�ʤ����Ȥ�ʬ����ޤ���

�Ŀ�����ʬ�ϡ�1�����Ф��ι��פ����ޥ�����ꤹ�뤳�Ȥ��Ǥ��ޤ���
����ޥ����������Ǥ���Ȥ����ޥ��Ȥ���ޤ��Ȥ��������ꤷ̷�⤹��Ȥ��β�ǽ����̵�����Ȥ�ʬ����ޤ���
2n-1�ζ�֤�n�Ĥι��ޥ�������Ȥ���ȡĤȤ���ñ�㲾�����ʬ����Ȥ��ˤ褯����ޤ���
�äˤ���ޥ�����ޥ��Ȳ��ꤷ��̷�⤷���餽�Υޥ�����ޥ�����ޥ��Ȳ��ꤷ��̷�⤷������ޥ��Ǥ���
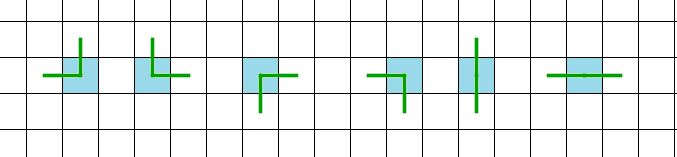
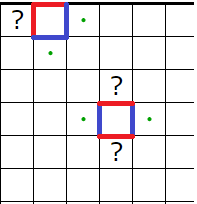
�ʲ��������Ĥ������Ƥߤޤ���
������ǽƤ����ü��ˡ�פȤ�����ڤ�������ȯŸ����Ԥ˽Ƥ���ޤ���
���ޥ��Ǥ���Ȳ��ꤷ��̷�⤹���㭡�ʾ��롼�ء�

�忧�Υޥ��Ϲ��ޥ��Ȳ��ꤷ����������Ƥߤ�Ⱦ��롼�פ������̷�⤹��Τǡ���ޥ��Ǥ��뤳�Ȥ�ʬ����ޤ���
���ޥ��Ǥ���Ȳ��ꤷ��̷�⤹���㭢��ü��ˡ��

�忧�Υޥ��Ϲ��ޥ��Ȳ��ꤹ��Ⱥ������ʬ����������ü�ο�������ܤˤʤ뤿��̷�⡢��ä���ޥ���ͭ�뤳�Ȥ�ʬ����ޤ���
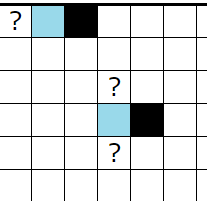
��ޤ��Ǥ���Ȳ��ꤷ��̷�⤹���㭡�ʾ��롼�ء�

�忧�Υޥ�����ޥ��Ȳ��ꤷ����������Ƥߤ�Ⱦ��롼�פ������̷�⤹��Τǡ����ޥ��Ǥ��뤳�Ȥ�ʬ����ޤ���
��ޤ��Ǥ���Ȳ��ꤷ��̷�⤹���㭢��ü��ˡ��

�忧�Υޥ�����ޥ��Ȳ��ꤷ����������Ƥߤ�Ⱥ������ʬ����������ü�ο�������ܤˤʤ뤿��̷�⡢��äƹ��ޥ���ͭ�뤳�Ȥ�ʬ����ޤ���

���礦�ɣ������ɤ��äƤ���ޥ��ϡ����ܤ���ޥ��Τ����ɤ��äƤʤ������ˤ���ޥ�����ޥ��Ǥ��뤳�Ȥ�ʬ����ޤ���
���դ���ʬ����Ť餤�ΤǤ����㤨�о�ޤǡ����ǤäƤ���ޥ��������ǡ��º���ޥ��ˤʤ�ޤ���

��ͳ�Ϲ��ޥ���ñ�㲾�ꤷ�Ƥߤ��ʬ����ޤ������忧�Υޥ������̤줺�ι��פˤ����ޥ��ˤʤ�Τǹ��ޥ���Ϣ³����̷�⤹�뤫��Ǥ���

�äˡ�������֤����̤ˤ����ƳѤ��٤οޤǡ����ǤäƤ���ޥ��ϤϤ��ᤫ����ޥ��ʤΤ����ꤷ�Ƥ��ޤ���
���礦�ɣ������ɤ��äƤ���ޥ������ĥ��ƥ襳��Ϣ³���Ƥ���Ȥ��������Υޥ��������̤뤳�Ȥ�ʬ���ꡢ���������ΰ����������ꤷ�ޤ���
��

�㤨�о�������������ǰϤޤ줿��ʬ��ͤ��ޤ��������Ϻɤ��äƤ��������������Ϻɤ��äƤ��ʤ�������ɽ���Ƥ��ޤ���Ϣ³����ޥ��Τ��������ˡ�ñ�㲾��α��ѡʽи��������ˡפ�Ȥ��Ȥ⤦��������ޥ��Ǥ��뤳�Ȥ��狼�ꡢ�⤦�������Ф��ơ�ñ�㲾��α��ѡʽи��������ˡפ�Ȥ�����������ޥ��Ǥ��뤳�Ȥ�ʬ����ޤ���

��䤳���������ޤ���������������������ǰϤޤ줿�ޥ��Ϥɤ������ޥ��Ǥ��뤳�Ȥ����ꤹ��Ȥ������ȤǤ��������Ǥ��礦�ɣ������ɤ��äƤ���ޥ��Ǥ⤢�ä��Τǡ��������ꤷ�ޤ���

����ü���飲���ܤιԡ���ˤϡʤ��ιԡ���䤽�ζ������ü�ιԡ���˥ҥ�Ȥ�̵�����ˤϡˣ������Ф��ǤϹ��ޥ���������ޤ���äƹ��ޥ��������ʤ飲�����Ф��ʾ�ˤʤ�ޤ����ʡ��ɺ������פǡ��դ������פ�����Ƥ�����⤢��Τ��ʤȻפä��ΤǤ�������ͳ�Υ����å����㤦�����̤Τ�ΤȤ��ư����ޤ�������
��ͳ:

�ºݣ������Ф�������Ƥߤ�����λ���ϩ��ȯ�����Ƥ��ޤ�̷�⤹�뤫��Ǥ���
�����������ιԡ���䤽�ζ������ü�ιԡ���˥ҥ�Ȥ�̵����֤ξ�����äʤΤǡ����Τ褦�ʥҥ�Ȥ������磱�����Ф��Ǥ��֤��뤳�Ȥ⤢�뤳�Ȥ����դ��Ƥ���������

���ν����꤬����ʾ�Ǥ��ʤ����ڡ����������������ü�θĿ��϶����ܤǤʤ��Ȥ����ʤ��Ȥ���ˡ§�Ǥ���
������������Ȳ��ꤷ����硢�ɤΤ褦������ü�äĤ����Ȥ��Ƥ⣱������ü��;�äƤ��ޤ����Ȥ���ʬ����ޤ���
�ºݤλȤ����Ȥ��Ƥϡ����Σ�����Τ��������ä���Ф뤳�Ȥ��Ǥ�������Ǥ����������̤�뤫�����������Ϥɤ��ʤ뤫����ꤹ�뤳�Ȥ��Ǥ��ޤ���
����������ҤΡ�ñ�㲾��פι�ˤ⤢��ޤ����������Ǥ⣱�ľҲ𤷤����Ȼפ��ޤ���
��

�㤨�Ф���ʾ������ä��Ȥ��ޤ���

�ִݤ�����ü�ڤӲ��п��Υ��ڡ�����ͤ���ȡ����Ȳ��п��Υ��ڡ����˽�����Ǥ�������ü���ִݤΤߤǤ��������п��Υ��ڡ����ˤ�������ü���ܿ��ϣ��ܡʴ���ܡˤΰ٤��ȣ�������ü��������ޤʤ���̷�⤹�뤳�Ȥˤʤ�ޤ���

��ä��ִݤ�����ü�ϱ��˹Ԥ����Ȥ�ʬ����ޤ�����
ü��ˡ�ϱ����ϰϤ������Ǥ����������ǤϹ��ޥ�����ߤΣ����Ҳ𤷤ޤ���
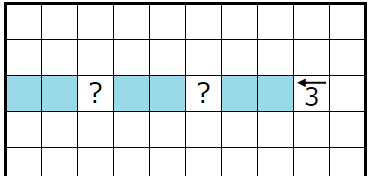
�㣱

��������������ͤ��ޤ��������Ǥϣ�����ͤ��ޤ���

�����Υҥ�Ȥ��������ϣ��̤ꤢ��ޤ�����

���Σ���˴ؤ��ƿ忧����ʬ��ͤ��Ƥߤ�ȡ����ν�����Ϥ⤦�Ǥ��ޤ�������ü������ܡʣ��ܡˤˤʤäƤ���Τ�̷�⡣

��äƣ����Υҥ�Ȥǹͤ�������ޥ����������Σ��̤��棲�̤꤬������ä��ΤǻĤ���ޥ����������dz��ꤹ�뤳�Ȥˤʤ�ޤ���
�㣲

��������������ͤ��ޤ���

�����Υҥ�Ȥȡ��忧�γ�1��2����ʬ��������ޥ���¿����顢��1��2����ʬ�ˤϣ��Ĥ��Ĺ��ޥ������뤳�Ȥ�ʬ����ޤ���


��1��2�ޥ��Τɤ���˹��ޥ�������Ƥ⡢������ˤ�������п��ζ��֤ˤϳƣ��ܤ��ġ��ף��ܹ��ޥ���������ळ�Ȥ�ʬ����ޤ���
�ޤ�������п�����ʬ�Ǥ����������ꤳ��;�Ϥ�����Τϥԥ��Υޥ��ΤߤǤ��뤳�Ȥˤ����դ��ޤ���

��äơ��ԥ��Υޥ�����ޥ��Ȳ��ꤹ��ȡ�����п�����ʬ�������������ü�ϣ��ܡʴ���ܡˤȤʤä�̷�⤷�ޤ���

�ʾ���ԥ��Υޥ��Ϲ��ޥ��Ǥʤ��Τ������̤�ޥ��Ǥ��뤳�Ȥ�ʬ���ꡢ���Τ褦���������ꤷ�ޤ���
���롼�ؤ�¾�������ڤ�ü������/���ޥ������Ǥ������ʤ�����ޥ����������������ʬŪ�˥롼�פ��äƤϤ����ʤ��Ȥ�����ڤǤ����������ǤϾ��롼�ؤ��ͤ�����辮�롼�ؤ�������ޥ������Ǥ������ʤ����ڡ����ˤϡ����Υ��ڡ�������Ὢ���ޤdz�����������ꤹ������ü�����ʤ��Ȥ�2�ܤ�¸�ߤ��ʤ���Фʤ�ʤ��ʤǤʤ��ȳ���ʬ�ˤɤ����Ƥ⾮�롼�פ�������ˤ��Ȥ����ޤ��ڤΤ��ȤȤ��ޤ���
�狼��Ť餤�Τ����Ф��ޤ���
��

���Τ褦�ʾ�����ͤ��ޤ���

��¦����ʬ�⺸¦����ʬ����ޥ������Ǥ������ʤ��ΤǤ��Τ褦�������̤뤳�Ȥ�ʬ����ޤ���

�ޤ��ԥ��Υޥ�����ޥ��Ȳ��ꤷ����������ȡ���¦�Υ��ڡ����Ǥɤ��Ĥʤ��������롼�פˤʤ�Τǹ��ޥ��ˤʤ�ޤ���
�ޤ�������ʷ�ޤ����⤢��ޤ���


�ڥ�ѥ���Τ���«�Ȥ��Ƥ��������ͣ���Ǥ����ͣ���Ǥʤ��ʤ�����������Ǥ���ˤȤ����Τ�����ΤǤ����������ռ�ˤȤä����̤�ʤ餳��������ޤ����뤷���ʤ��������Ȥ���������Ǥ�����ڤȤ���������̯�Ǥ����ġ�
���ա�
�ֲ褦�˺��פȤ����褦�˺��������ͣ������Ȥäƹ��ޥ�����������Τϴ����Ǥ����ʤ��ʤ餽�Υѥ��뤬ͣ���Ǥ��롢�Ȥ������Ȥ�����Ȥ���������Τ��ᡢ��äƤ����ʳ���ͣ���ʬ����ʤ����֤ǤϻȤ��ʤ�����Ǥ���
������������줷���ʤ�����ѥ�����ˤʤ뤳�Ȥ⤢��ޤ����ġ�
�����ǤϺ����ˤ���ˤ�褯�ФƤ���ѥ������Ҳ𤷤ޤ���

����Ǥ���

�������뤿�������ü�ˤ��줾������¡��á��ĤȤ���̾�����դ��ޤ���

���ȣ¡��äȣĤ�Ĥʤ��Ĥʤ����ϣ��̤ꤢ��Τ�����β�ͣ���ʤ���ȣ¡��äȣĤ�Ĥʤ����Ȥ�̵����ʬ����ޤ���

���ȣ¡��äȣĤ�Ĥʤ��ǤϤ����ʤ���ʬ����Ф��Τ褦�����������뤳�Ȥ�ʬ����ޤ���
��������äƤ��Ƥ��Υѥ����Ф���ᤷ���ġ�
��äƤ���Ȥ��ˤ��Υѥ����Ф�ȳ������龮�롼�ؤǤ�����ʬ�����Ǥ���褦�ˤ��ʤ��Ȥ����ʤ��ΤǤȤƤⵤ���ޤ������⤦������ʬ��ä��ƿ����ͤ��ʤ������Ȥ������Ȥ�ͤ��ޤ���
�ޤ����֤Σ��ޥ���ҥ�Ȥ�����Ȥ���Ķ�ϵ��⤢��ޤ����ġ�
�Ǹ�μ��ʤǤ������ꤷ�����Τޤ���ǤⲾ�ꤷ�Ʋ��Ǥ��������Ȥ�ʤ���вʤ�����ϴ���Ū�ˤȤƤ����Ǥ���
��Х�������٤��ȤƤ�⤤��Х��䥸���λ��Ǥ����ͤˤ�äƤɤ������Х��Ȥ��뤫�Ͻ��⤢��ޤ��ˤϤ����Ȥ�ʤ��Ȳʤ����Ȥ�¿������ޤ���
�����ˤ�䥸���μ�ڤˤĤ��ƽƤ��뵭����ޤȤ¸�ߤ��ޤ��ΤǾҲ𤵤���ĺ���ޤ������Υڡ����˽Ƥ��ʤ���ڤ⤢��ޤ��Τ�����������������
��Х���ڽ�(�ʰ���)--SP1�ΤѤ���ˤä�
SP1��ˤ��䥸����ڽ��Ǥ�����Х��Ȥ���ޤ�������Х��䥸���Τ��ȤʤΤǥ䥸���Ǥ���
�䥸����ڤޤȤ�
�դ����ߤΤ���ˤ��䥸����ڽ��Ǥ���