「手筋」というのは、簡単に説明するとパズルを解く際のノウハウのことです。
ここでは、天体ショーを実際に解いていく上で役立つ、汎用性の高い（と思われる）手筋を挙げていきます。
なお本ページではいわゆる通常の正方格子の長方形盤面を前提として説明を記述します。一部の手筋はハニカム等や高次元立方格子でも成立します。
ここでは、天体ショーを実際に解いていく上で役立つ、汎用性の高い（と思われる）手筋を挙げていきます。
なお本ページではいわゆる通常の正方格子の長方形盤面を前提として説明を記述します。一部の手筋はハニカム等や高次元立方格子でも成立します。
手筋とは少しく異なるため詳しくは書きませんが、上記２つだけによって確定する構造は天体ショーにおいて頻出なので、普段から見るようにしていると見つけやすくなります。
複数の表出*2が集まった領域をまとめて一つの手筋とみなすというスタイルになります。
線を引くときに一筆書きで引くようにすると快適に解くことができます。
複数の表出*2が集まった領域をまとめて一つの手筋とみなすというスタイルになります。
線を引くときに一筆書きで引くようにすると快適に解くことができます。
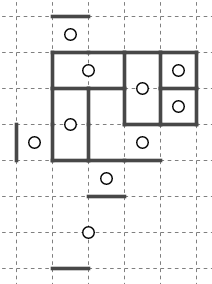
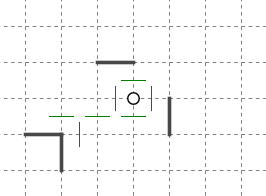
天体ショーでは全てのマスが最終的にいずれかのブロックに入る必要があります。
これはマス側からすれば、自分を入れてくれるブロックの親元に当たる星をどうにか探す、ということになります。
一方星側からすれば、空間に散らばった行きどころのないマス達を星どうしで分け合って余す所なく回収する、ということになります。
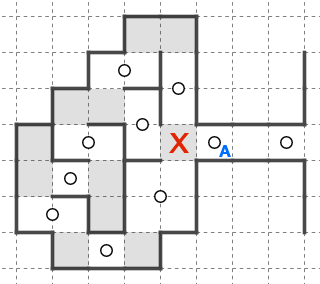
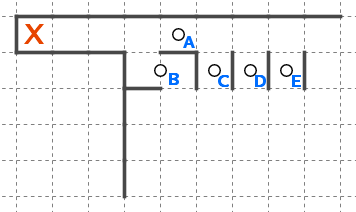
上の例で考えてみましょう。
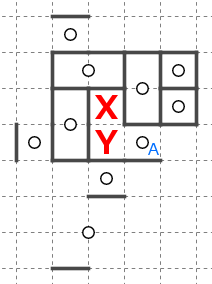
マスXとマスYはまだ親星*3が決まっていません。
星Aのブロック以外の接触境界は全て蓋がされてしまっていますから、星Aのブロックに入ることが確定します。
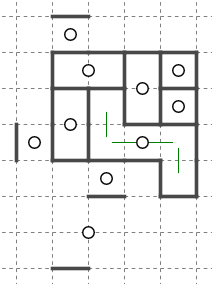
ブロックA（星Aのブロック）が確定しました。
この時、「マスXは（マスYは）星Aに回収された」または「マスXは（マスYは）ブロックAに回収された」と呼ぶことにします。
回収周りの手筋を完全に分類するのは難しい話になるかと思いますが、最も単純な回収は上のように、星のない閉じられた空間に対して出入り口が一箇所あるような場合です。
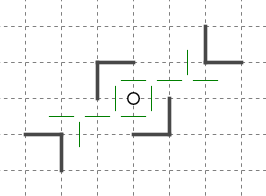
ある星があるマスを回収できるかを判断する際に核となる論理が、回収可能性判定です。
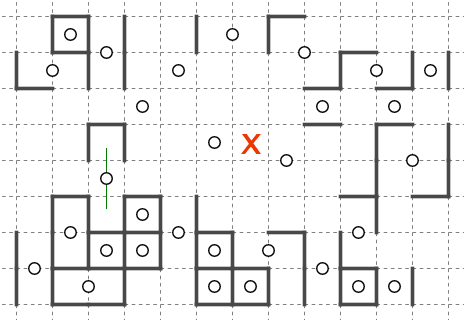
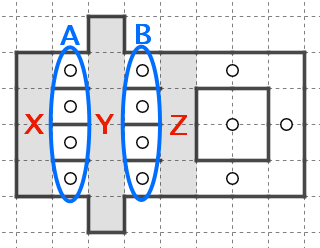
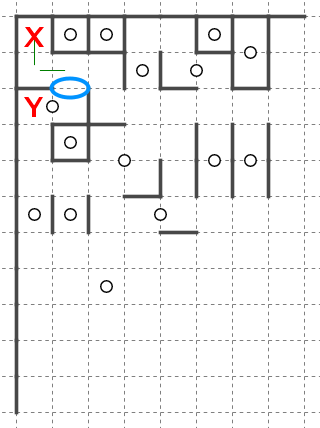
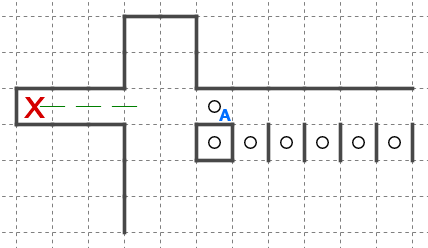
このような状況でマスXがどの星に回収されうるか考えます。
マスXとつながっている未回収なマスのかたまり（図で黄色に塗った領域）に注目します。未回収なマスのかたまりを未回収クラスタと呼んでいます。
未回収クラスタに接しているブロックの集合（青色のブロック集合）はマスXを回収する可能性がありますが、離れている星、例えば星Aや星Bは回収することができない、ということがお分かりいただけるかと思います。天体ショーのブロックはひとつながりである必要があるためです。青色の部分で盤面は「分断」されています。したがって親の候補は青色のブロックの星に絞り込むことができます。
これは言いかえると、星からマスへの（タテヨコにひとつながりの）経路が少なくとも１つ存在しなければならない、ということになります。
ブロックAやブロックCのように完全に周囲に線が引かれたブロックは既に確定しきっていますから、それ以上大きくなることはできません。このためAやCのような星は候補から外せます。
またGのように、注目している未回収クラスタに対する全ての接触部分に既に線が引かれていれば、その星も候補から外せます。
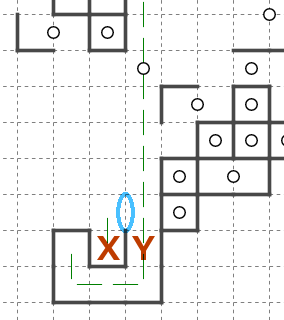
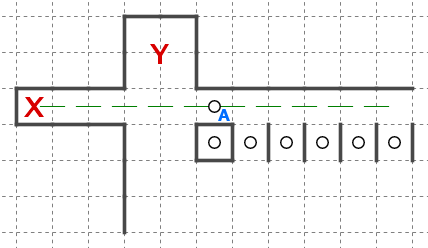
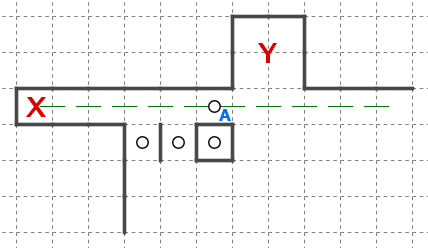
ブロックFがマスXを回収できるかどうかを考えます。
マスXの対称位置（マスY）が他のブロックに回収されることが既に確定しています。天体ショーのブロックはマスを対称に回収する必要があり、他のブロックとはマスを共有できないため、マスXがブロックFに入らないとわかります。
Eは回収できそうですが、Dはどうでしょうか。
この場合、画像で示している範囲では判断ができません。マスXの対称位置が、Fのケースのように他のブロックに回収されていれば回収できません。また、マスXの対称位置が盤面の範囲外にある場合も回収ができません。
このような状況でマスXがどの星に回収されうるか考えます。
マスXとつながっている未回収なマスのかたまり（図で黄色に塗った領域）に注目します。未回収なマスのかたまりを未回収クラスタと呼んでいます。
未回収クラスタに接しているブロックの集合（青色のブロック集合）はマスXを回収する可能性がありますが、離れている星、例えば星Aや星Bは回収することができない、ということがお分かりいただけるかと思います。天体ショーのブロックはひとつながりである必要があるためです。青色の部分で盤面は「分断」されています。したがって親の候補は青色のブロックの星に絞り込むことができます。
これは言いかえると、星からマスへの（タテヨコにひとつながりの）経路が少なくとも１つ存在しなければならない、ということになります。
ブロックAやブロックCのように完全に周囲に線が引かれたブロックは既に確定しきっていますから、それ以上大きくなることはできません。このためAやCのような星は候補から外せます。
またGのように、注目している未回収クラスタに対する全ての接触部分に既に線が引かれていれば、その星も候補から外せます。
ブロックFがマスXを回収できるかどうかを考えます。
マスXの対称位置（マスY）が他のブロックに回収されることが既に確定しています。天体ショーのブロックはマスを対称に回収する必要があり、他のブロックとはマスを共有できないため、マスXがブロックFに入らないとわかります。
Eは回収できそうですが、Dはどうでしょうか。
この場合、画像で示している範囲では判断ができません。マスXの対称位置が、Fのケースのように他のブロックに回収されていれば回収できません。また、マスXの対称位置が盤面の範囲外にある場合も回収ができません。
緑のマスの親星は確定しますが、そのマスと親星をどうつなぐかはこれだけでは確定しません。
しかし緑のマスを回収すること自体は確定するため、右下で手が進みます。実際の回収方法は後で戻ってきたときに確定することになります。
天体ショーを仮定で解く際に、代表的な仮定として、成長の促進に対応する仮定と、成長の抑制に対応する仮定が挙げられます。
ここで成長促進の仮定とは、ある星（星群）があるマス（マス群）を回収する、という仮定を指します。抑制仮定は逆にマスを回収しないと仮定するものを指します。
仮定の結果としてブロックが大きくなる、すなわち成長する、というイメージからこのように呼んでいます。天体ショーの場合は全てのマスを余すことなく星で分け合うという性格なので、成長促進と成長抑制は表裏一体の概念になります。
これら以外の仮定としては、二つのマスが同じブロックに入るかどうかという観点の仮定が挙げられます。
ここで成長促進の仮定とは、ある星（星群）があるマス（マス群）を回収する、という仮定を指します。抑制仮定は逆にマスを回収しないと仮定するものを指します。
仮定の結果としてブロックが大きくなる、すなわち成長する、というイメージからこのように呼んでいます。天体ショーの場合は全てのマスを余すことなく星で分け合うという性格なので、成長促進と成長抑制は表裏一体の概念になります。
これら以外の仮定としては、二つのマスが同じブロックに入るかどうかという観点の仮定が挙げられます。
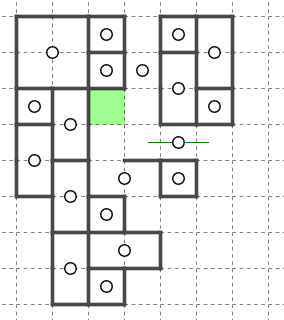
この局面は、今しがたマスXが星Aに回収されることが確定したところです。
ここで回収経路を考えることで直ちに決まる部分があります。
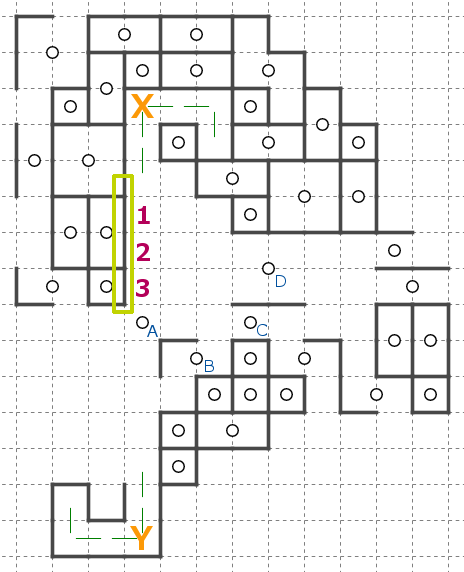
星AからマスXに向かう部分は片側が壁でつながっています。
右側には星B、C、Dがありますが、それらの星のさらに右側を星Aが回り込むことはできません。
このため、壁沿いのマス1、2、3は星Aが回収することが確定します。
回収経路を確保する手筋は様々な形態がありますが、その中でも上のように壁沿いに回収する手筋は比較的わかりやすいものとなっています。
上で説明した論理で成立しているため、壁でつながっていれば必ず適用できる手筋ではないことに注意が必要です。
この手筋は壁に多少凹凸や曖昧性があっても適用できる場合があります。その場合は難しい手筋となります。
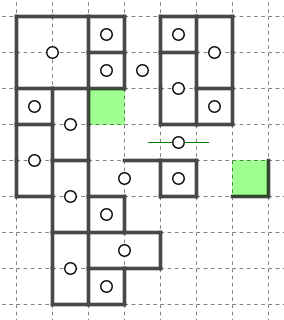
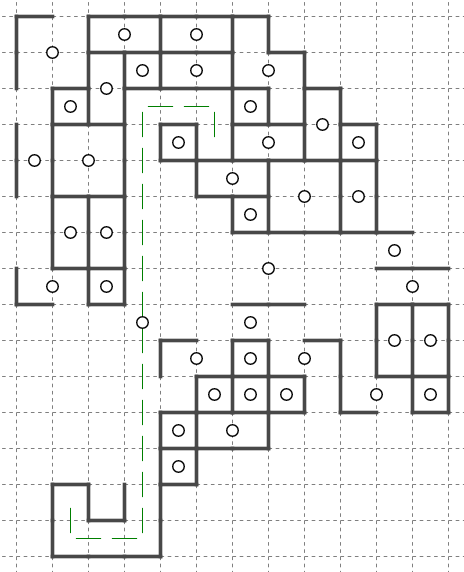
マスXが閉じ込められないように上方向に脱出してきました。マスYのブロックと接触（辺接触）します。
マスXのブロックとマスYのブロックは脱出を始める前から既に接触済みだったことに注意します。
接触部分には壁があったため、これらが異なるブロックに入ることは既に分かっています。
したがって丸で囲った部分にも壁が入ることが分かります。
イメージとしてはn個のブロックが狭い領域からお互いを圧迫しながら一気に脱出する、というものが一般に押し合い（押し出し、追いかけっこ等）と呼ばれますが、天体ショーでは親星が確定する前に異なるブロックに入ることが確定することは稀なため、１つを除くブロックの親が確定している場合や、全ての親が確定している場合に使われる場合が多いです。
天体ショーの場合は、上図のように脱出と組み合わせて迷子を大きくするのによく使われます。
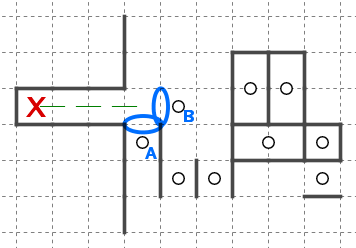
こちらはより原理的な例です。星Aや星Bは迷子Xを回収できないため、これらは異なるブロックになります。したがって間に線を引くことができます。
（私は押し合い手筋の感覚として、既に接触しているブロックが再接触するという点を重視しており、この手筋は後述の破綻閉じ込めに分類していますが、原理は同じです）
鍵となる論理はブロック同士の接触で生じる壁と本質的に同じですが、こちらの場合は片方のブロックが迷子なので少し見え方が異なるのがポイントです。
天体ショーを解いていると、周囲のほとんどを囲まれた領域、というものが良く出てきます。
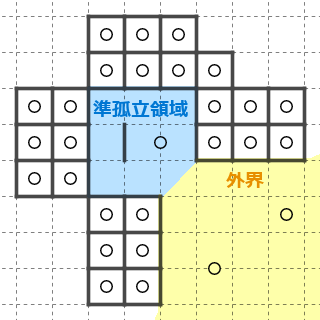
ここではこういった周囲を圧迫された領域を、準孤立領域と呼ぶことにします。
準孤立領域と外界との相互作用として生じる手筋の一つが迷子の脱出でした。迷子の脱出は「準孤立領域が積極的に外界と相互作用しようとする手筋」と言えます。
これに対して、準孤立領域が外界との相互作用を拒む形の手筋を鎖国と呼んでいます。
例を挙げます。
マスXを外界にある星が回収するには、中線列で示した経路を通る必要があります。
しかしそこを通ってしまうと、薄紅色で塗った領域がどのブロックにも入らない状態になってしまいます。
したがってマスXはこの準孤立領域の内部で回収することが確定します。
この決まり方はブロッキングの一種と解釈することもできます。また、後述の破綻閉じ込めの一種とも言えます。鎖国は、特定の親に対してではなく外界にある全ての星について回収できないことがわかる点が強力です。
ここではこういった周囲を圧迫された領域を、準孤立領域と呼ぶことにします。
準孤立領域と外界との相互作用として生じる手筋の一つが迷子の脱出でした。迷子の脱出は「準孤立領域が積極的に外界と相互作用しようとする手筋」と言えます。
これに対して、準孤立領域が外界との相互作用を拒む形の手筋を鎖国と呼んでいます。
例を挙げます。
マスXを外界にある星が回収するには、中線列で示した経路を通る必要があります。
しかしそこを通ってしまうと、薄紅色で塗った領域がどのブロックにも入らない状態になってしまいます。
したがってマスXはこの準孤立領域の内部で回収することが確定します。
この決まり方はブロッキングの一種と解釈することもできます。また、後述の破綻閉じ込めの一種とも言えます。鎖国は、特定の親に対してではなく外界にある全ての星について回収できないことがわかる点が強力です。
仮定や先読みは比較的難易度の高い問題に取り組む際に役立つ考え方です。
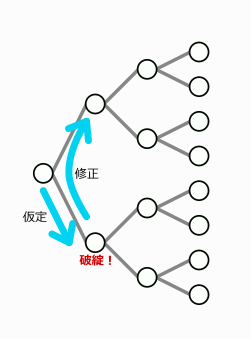
２個（もっと多い場合もあります）の選択肢の内、選択肢Aを選択すると破綻するのでAは正しくない、と背理法で推論する手法を仮定と呼んでいます（もう少し柔軟な仮定の使い方もあります。これについては後述します）。
上図の例では仮定をして直ちに破綻に気付けていますが、一般には解き進めないと破綻に気付けない場合もあります。
また、時には仮定を多重に行うこともあります。
※解または解の一部がルールに抵触すること、または解がなくなることを破綻（ハタン）すると言います。この言葉は作問*4の文脈でも使われることがあります。複数解になることを破綻と呼ぶ場合もあります。解消*5ができない破綻のことのみを破綻と呼ぶ場合もあります。縛りのある作問で縛りを満たす問題が作れない場合に破綻と言う場合もあります。
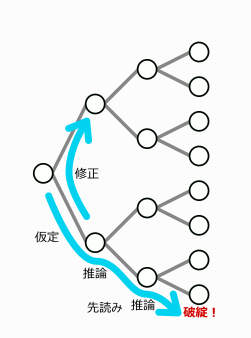
先読みは仮定を行うための方法論の一つで、基本的には仮定をした後のいくつかのステップを紙面やプレイヤー上に書き込まずに目解き*6で完結することを指します（目解きに限らず一般に仮定後の推論を先読みと呼んでいる場合もあるようです）。
天体ショーの場合、特に読むのが簡単な推論として、いわゆる連鎖が挙げられます。連鎖というのは入口と基礎知識と単純な回収で説明した論理を中心とした簡単な推論だけで手が進むものです。２〜３連鎖で破綻する構造は実際の問題で時々見かけます。
このセクションで述べたような硬い仮定（理詰め*7色の強い仮定）を行う立場としては、見つけた選択肢の内、最も「不正解」に思える選択肢をあえて試して、矛盾が現れるのをまだかまだかと期待しながら手を進めることになります。あるいは、比較的先読みしやすい選択肢から試す、というのも一つの戦略です。
鎖国や破綻閉じ込めは仮定によってとらえられる考え方です。勿論他の手筋も仮定で説明することは可能です。これは認識の問題になります。
「いずれにせよ」はある選択場面において、どちらを選んでも推論の結果同じ選択が生じる場合に、先に推論先の部分を確定する手筋を指します。予約と感覚的には離れていますが関連の強い考え方です。
例えばこのような状況を考えます。
マスXを回収するのは星Aまたは星Bのいずれかです。しかしいずれにしても星C、D、Eの出入り口は塞がれます。したがって…
このように星C、D、Eの上下に線を引くことが出来ます。
２個（もっと多い場合もあります）の選択肢の内、選択肢Aを選択すると破綻するのでAは正しくない、と背理法で推論する手法を仮定と呼んでいます（もう少し柔軟な仮定の使い方もあります。これについては後述します）。
上図の例では仮定をして直ちに破綻に気付けていますが、一般には解き進めないと破綻に気付けない場合もあります。
また、時には仮定を多重に行うこともあります。
※解または解の一部がルールに抵触すること、または解がなくなることを破綻（ハタン）すると言います。この言葉は作問*4の文脈でも使われることがあります。複数解になることを破綻と呼ぶ場合もあります。解消*5ができない破綻のことのみを破綻と呼ぶ場合もあります。縛りのある作問で縛りを満たす問題が作れない場合に破綻と言う場合もあります。
先読みは仮定を行うための方法論の一つで、基本的には仮定をした後のいくつかのステップを紙面やプレイヤー上に書き込まずに目解き*6で完結することを指します（目解きに限らず一般に仮定後の推論を先読みと呼んでいる場合もあるようです）。
天体ショーの場合、特に読むのが簡単な推論として、いわゆる連鎖が挙げられます。連鎖というのは入口と基礎知識と単純な回収で説明した論理を中心とした簡単な推論だけで手が進むものです。２〜３連鎖で破綻する構造は実際の問題で時々見かけます。
このセクションで述べたような硬い仮定（理詰め*7色の強い仮定）を行う立場としては、見つけた選択肢の内、最も「不正解」に思える選択肢をあえて試して、矛盾が現れるのをまだかまだかと期待しながら手を進めることになります。あるいは、比較的先読みしやすい選択肢から試す、というのも一つの戦略です。
鎖国や破綻閉じ込めは仮定によってとらえられる考え方です。勿論他の手筋も仮定で説明することは可能です。これは認識の問題になります。
「いずれにせよ」はある選択場面において、どちらを選んでも推論の結果同じ選択が生じる場合に、先に推論先の部分を確定する手筋を指します。予約と感覚的には離れていますが関連の強い考え方です。
例えばこのような状況を考えます。
マスXを回収するのは星Aまたは星Bのいずれかです。しかしいずれにしても星C、D、Eの出入り口は塞がれます。したがって…
このように星C、D、Eの上下に線を引くことが出来ます。
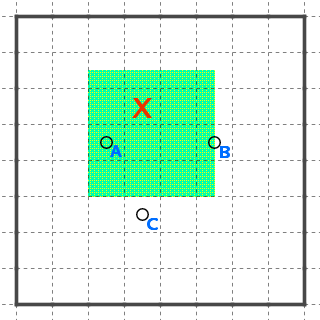
マスXは左側に大きく凹んでおり、わかりやすい迷子です。その右側の目立つ場所には星Aが置いてあります。
Xを星Aが回収できるか考えてみましょう。
マスXを星Aが回収すると仮定すると、このように中線が引け、領域Yは広い空間から分離されてしまいます。
こうなると領域Yはいずれのブロックにも入らなくなるためルールに反します。したがってマスXは、ブロックAに入らないことが確定します。
この例のように、仮定の結果として閉じ込められた領域が破綻する形の背理法を破綻閉じ込めと呼んでいます。
重要なのは仮定の結果として盤面が分断される点です。分断されなければすぐに破綻と気づくのは難しいですが、分断する仮定の場合は小さい空間だけを考えれば良いため、目解きで破綻まで読める場合も多くなりましょう。
この手筋の形は迷子の合流や、押し合い手筋の形に似ていますが以下のように違いがあります。迷子の合流の場合、準孤立領域として出入り口が十分狭いものを考えるのが普通です。上の例ですと領域Yの出入り口が広いため迷子が合流することまで確定しません。押し合い手筋が成立するためには領域Xと領域Yが異なるブロックに入る保障が先に必要ですが、この例にはその保障がありません。
破綻部分が星から見て仮定部分と逆にあっても同じ手筋が使えます。
この場合はXを回収すると破綻する、と考えずともXの反対側のマスを回収すると仮定して破綻を発見することもできます。
ですから上の例と本質的な違いはないのですが、この例のようにXのへこみ部分に視線が誘導されている場合は通常X側から解くことになります。その場合は「先読み」をすることになります。
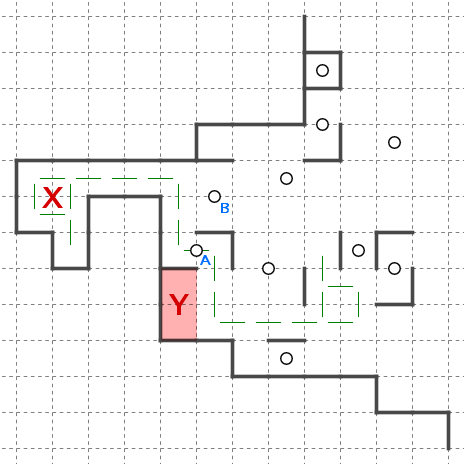
破綻閉じ込めのもう少し大きい例です。
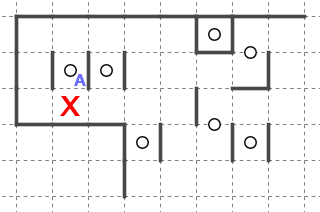
破綻閉じ込めの中でも、このような形で出てくるものは特徴的なので覚えておくと役立つでしょう。
マスXを星Aが回収すると仮定してみます。
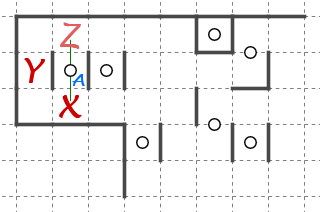
マスYが取れなくなります。
星AがマスXと、その反対のマスZを両方とも取ることによって経路がふさがれるため、この種の形を特別に対称破綻閉じ込めと呼んでいます。
特に幅３の長方形型はわかりやすく特徴的なので覚えておくと良いでしょう。
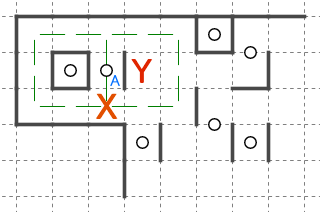
この形は対称破綻閉じ込めの直後に使わていることがあります。
迷子が大きくなってくるとこのように大規模な破綻閉じ込めが空中*8で生じる場合もあるので、迷子の出入り口付近に星があればまずは軽く先読みを試してみると良いでしょう。ただし作者によってはそういった仮定を潰した上で他の場所にもっと軽い理詰めを用意していることもあるので、無理そうなら別の場所を試すくらいの心持ちでも良いかと思います。
天体ショーのブロックは、星が乗っているマスを除いて常に偶数マスしか回収できないという性質を持っています。このため、星がいくつあっても奇数マスを回収することはできません。
上図では、この狭い領域に未回収のマス（灰色のマス）が11個残っています。パリティ（偶奇）の辻褄を合わせるために外側からXのマスを回収します。
このような局面を考えます。
星群Aと星群Bが３つのクラスタX、Y、Zを分断しています。
星群Aにある星について、左側の領域Xからnマス取る時、必ず右側の領域Yからも同じnマス取ることに注意すると、星群A全体で見ても左右の回収マス数は一致することがわかります。
今、星群A全体で左から4マス取ることは確定していますから、星群Aは右の領域Yからも4マス取ります。
領域Yで残った2マスはさらに右側の星群Bが回収するとわかります。同じ論理から、星群Bは領域Zから2マス取ることがわかります。
このように星群単位で取るマス数を分け合う考え方を譲り合いと呼んでいます。意外と応用パターンの多い考え方です。
盤面の隅近くにある星はどんなに頑張っても一定以上離れたマスを回収できません。
例えば上の星AはマスXは回収できますがマスYは回収できません。回収できる領域を網掛けしています。
逆に、あるマスXに注目した時、そのマスの親となれる星の存在できる領域も制限されます。
MxN長方形盤面の場合、最大の回収可能範囲（境界を含む）は(M-1)/2x(N-1)/2の長方形になります。
この考え方は星の密度が非常に少ない問題において効率良く候補を絞り込むのに役立ちます。
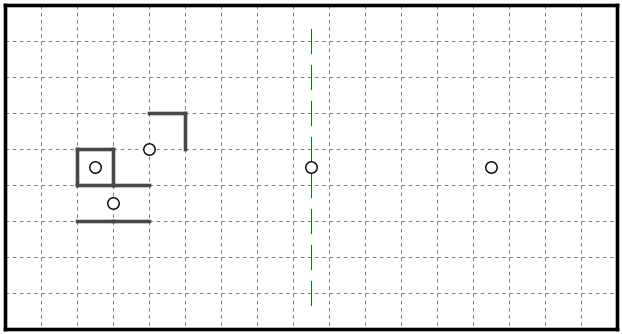
盤面が中央のブロックで分断されています。
星群ABCが作る図形が星Dの作る図形と異なるとすると、中央のブロックが点対称になってくれません。したがってこの二つの図形は同じ形になります。
このように座標軸を取ってみましょう。左側と右側で同じことが起こるということに注意します。
右側には星が一つしかないため、出来上がる図形はひとつながりな点対称図形で、かつ中心が星Dの対称位置にくる必要があります。
点対称な図形において中心は重心と一致することに注意します。
左側の３つのブロックA, B, Cの座標はそれぞれ(0.5,1.5), (1,0.5), (2,2)となっており、それぞれの面積をSA, SB, SCとすると重心の座標(xG, yG)は
(SA+SB+SC) xG = 0.5 SA + SB + 2 SC
(SA+SB+SC) yG = 1.5 SA + 0.5 SB + 2 SC
今右側の条件から(xG, yG)は(1.5, 1.5)であるとわかっているので、これを代入して整理すると
4 SA = 2 SB = SC
すなわちA、B、Cの面積比が1:2:4であることがわかります。今ブロックAの面積が1であることは既に分かっているので、B、Cの面積も確定します。
実際にこの形そのままで使用することはほとんどない手筋ですが、天体ショーを理解する上で重要な性質の一つと言えるかと思います。この問題の形の場合、後述の検証として使用することもできます。
パズルを解いている際にある仮定を行うと、解なしまたは複数解であることが確定してしまうという状況があります。
パズルの種類や状況にもよりますが、問題には解があり、なおかつ解が一つであると想定している場合は、その選択肢を棄却することが出来ます。
例を挙げます。
この問題は上下が対称になっています。
ここで、上下の対称性を破る解が存在すると仮定すると、その解を上下反転した状態も解として許されます。したがって解が複数になってしまいます。
したがってユニークネス手筋の考え方によって、解が上下対称であると確定します。
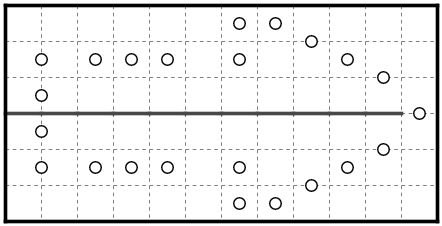
この場合はこのように中心に線を引くことができます。
星が対称線上にある場合、そのブロックは中心線に沿った２マスを同時に回収することができますが、他の星はそれが出来ないことに注意してください。
他の例を挙げます。
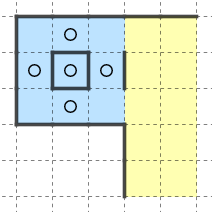
このような局所構造が大域と相互作用している系を考えます。
出入り口部分は下に挙げる二通りのいずれかとなります。
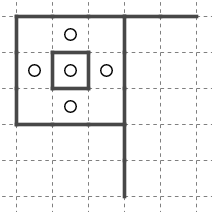
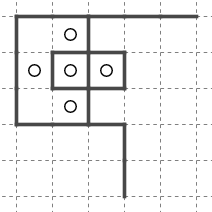
しかし上図一つ目の構造では局所的に複数解（または解なし）部分が閉じ込められてしまいます。
天体ショーではいったん壁で閉じ込められると外から遠隔で収束させることができません。部分に別解があると全体が別解または解なしになります。したがって解唯一性の仮定から二つ目の構造が想定解であるとわかります。
パズルの種類や状況にもよりますが、問題には解があり、なおかつ解が一つであると想定している場合は、その選択肢を棄却することが出来ます。
例を挙げます。
この問題は上下が対称になっています。
ここで、上下の対称性を破る解が存在すると仮定すると、その解を上下反転した状態も解として許されます。したがって解が複数になってしまいます。
したがってユニークネス手筋の考え方によって、解が上下対称であると確定します。
この場合はこのように中心に線を引くことができます。
星が対称線上にある場合、そのブロックは中心線に沿った２マスを同時に回収することができますが、他の星はそれが出来ないことに注意してください。
他の例を挙げます。
このような局所構造が大域と相互作用している系を考えます。
出入り口部分は下に挙げる二通りのいずれかとなります。
しかし上図一つ目の構造では局所的に複数解（または解なし）部分が閉じ込められてしまいます。
天体ショーではいったん壁で閉じ込められると外から遠隔で収束させることができません。部分に別解があると全体が別解または解なしになります。したがって解唯一性の仮定から二つ目の構造が想定解であるとわかります。
パズルを解く状況は様々です。
基本的にパズルを解く前に答えを見ることはしないという方が多いかと思います。それは純粋にパズルで答えを探す楽しみを損なう可能性があると考えられるためです。
しかし偶然見てしまう場合もあります。どうしても解けない場合に悔しいけれどいったん見て、改めて自力で解こう、という場合もあるかと思います。あるいは、一度解いたパズルだけれど面白かったのでもう一度解こう、というのも「答えを知っているパズルを解く」という状況になります。
この記事はパズルを解く際の方法論を書くという趣旨なので、このような状況の解き方についてもここで少し触れます。
人間がパズルを解く場合、意識的にせよ無意識にせよ、答えに関するなんらかの情報がある場合の思考は、全く情報がない場合の思考と異なります。
解の個数に関する情報に関しても同じことが言えます。例えば、有名なパズル作家様の作った問題で、何人ものプレイヤーに解きチェック*9されており、なおかつソルバーでも唯一解が確認されていれば、複数解や解なしのことを気にせず「安心して」解くということができましょう。解の個数に関する情報は当然解きに影響するのですが、欲しくないような状況でも多かれ少なかれ入ってきてしまう場合が多いです。
このように解き手に流入してくる（一定確率で正しい）情報をオラクルと呼んでいます。
答えに関する情報を得る手段として、直感というものもあります。
また別の例として、偶然発見というものがあります。これは、見つかった選択肢に対して仮定をしてみたら偶然答えを見つけてしまったという状況です。
解き手が答えに関する（正しいか厳密には分からない）情報を得る手段というのは大体この三つかと思います。
このような情報に対するスタンスは大きく分けて二つかと思います。一つは見つかったから解けた、というスタンスです。これは解きの時間短縮につながります。もう一つは、与えられた情報とは逆の仮定をして検証していく立場です。
ペンシルパズルは他のパズルと比して唯一解かどうかをかなり気にする方*10ですから、ペンシルパズルのWikiを見ている方は後者が多いかなと思います。
検証としては、上で述べたように仮定で地道に示していく他に重心計算や空間処理のセクションで記述しているような定理を利用してスマートに唯一解と証明できる場合もあります。
基本的にパズルを解く前に答えを見ることはしないという方が多いかと思います。それは純粋にパズルで答えを探す楽しみを損なう可能性があると考えられるためです。
しかし偶然見てしまう場合もあります。どうしても解けない場合に悔しいけれどいったん見て、改めて自力で解こう、という場合もあるかと思います。あるいは、一度解いたパズルだけれど面白かったのでもう一度解こう、というのも「答えを知っているパズルを解く」という状況になります。
この記事はパズルを解く際の方法論を書くという趣旨なので、このような状況の解き方についてもここで少し触れます。
人間がパズルを解く場合、意識的にせよ無意識にせよ、答えに関するなんらかの情報がある場合の思考は、全く情報がない場合の思考と異なります。
解の個数に関する情報に関しても同じことが言えます。例えば、有名なパズル作家様の作った問題で、何人ものプレイヤーに解きチェック*9されており、なおかつソルバーでも唯一解が確認されていれば、複数解や解なしのことを気にせず「安心して」解くということができましょう。解の個数に関する情報は当然解きに影響するのですが、欲しくないような状況でも多かれ少なかれ入ってきてしまう場合が多いです。
このように解き手に流入してくる（一定確率で正しい）情報をオラクルと呼んでいます。
答えに関する情報を得る手段として、直感というものもあります。
また別の例として、偶然発見というものがあります。これは、見つかった選択肢に対して仮定をしてみたら偶然答えを見つけてしまったという状況です。
解き手が答えに関する（正しいか厳密には分からない）情報を得る手段というのは大体この三つかと思います。
このような情報に対するスタンスは大きく分けて二つかと思います。一つは見つかったから解けた、というスタンスです。これは解きの時間短縮につながります。もう一つは、与えられた情報とは逆の仮定をして検証していく立場です。
ペンシルパズルは他のパズルと比して唯一解かどうかをかなり気にする方*10ですから、ペンシルパズルのWikiを見ている方は後者が多いかなと思います。
検証としては、上で述べたように仮定で地道に示していく他に重心計算や空間処理のセクションで記述しているような定理を利用してスマートに唯一解と証明できる場合もあります。
パズルを解いていくと最後に小さい領域が残ることがあります。
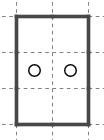
上のような形には頻繁に遭遇します。
そのたびにいちいち理詰めで考えるのは効率が悪いので、覚えておくと効率よく解くことができます。
私自身は覚えるのが得意ではないのであまりここに書けることはないのですが、いくつか私の知っているパターンを挙げます。
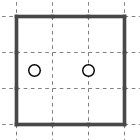
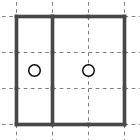
星が一列に並んでいるこのような形を川と呼んでいます。星が並ぶ構造は視認しやすいのでその性質を知っておくと解きが効率化できるでしょう。
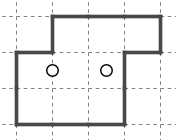
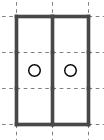
これなども良く見かけます。
このようなパターンに対してスッと線が引けるようになっておくと気持ちよく解き終えることができます。
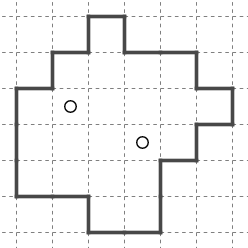
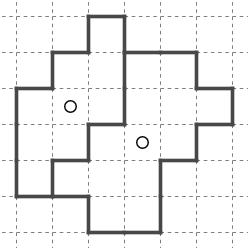
もう少し大きい構造になってくると記憶するのは難しくなります。
ただ、星が二つの場合切り方が複数になることはないので、ぱっと見えた切り方で解になっていれば別解を気にする必要はありません。
証明： 天体ショーが複数解になるためには偶数ノードの広義ループが存在する必要があります。ここで広義ループとはサイクリックなマスの列{Xi, i=1, 2, 3, ..., N}であり、マス列上で連続するどの２つのマスもその中点に星があるものです。複数解の場合に適当に選んだ二つの解の差分に注目することでこのループを作り出すことが常にできます。星が二つの場合、星の座標をrA、rBとするとループは２ノード進むたびに2(rA-rB)だけ並進します。偶数(2n, n>0)ノードでループが閉じるためには2n(rA-rB)がゼロベクトルである必要があります。これは不可能なので二つの星ではループが作れません。したがって星２つでは複数解になりえません。
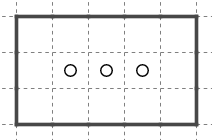
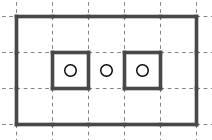
これは印象的な構造です。たまに見かけます。
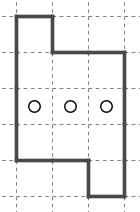
３ブロック以上の川だとこのように外側に少しだけひねりが入った形で見ることが多くなります。
このあたりも覚えておいて損はないと思います。
もっと沢山の星からなる空間処理も覚えていく、ということを考えるのも面白い挑戦かと思います。
上のような形には頻繁に遭遇します。
そのたびにいちいち理詰めで考えるのは効率が悪いので、覚えておくと効率よく解くことができます。
私自身は覚えるのが得意ではないのであまりここに書けることはないのですが、いくつか私の知っているパターンを挙げます。
星が一列に並んでいるこのような形を川と呼んでいます。星が並ぶ構造は視認しやすいのでその性質を知っておくと解きが効率化できるでしょう。
これなども良く見かけます。
このようなパターンに対してスッと線が引けるようになっておくと気持ちよく解き終えることができます。
もう少し大きい構造になってくると記憶するのは難しくなります。
ただ、星が二つの場合切り方が複数になることはないので、ぱっと見えた切り方で解になっていれば別解を気にする必要はありません。
証明： 天体ショーが複数解になるためには偶数ノードの広義ループが存在する必要があります。ここで広義ループとはサイクリックなマスの列{Xi, i=1, 2, 3, ..., N}であり、マス列上で連続するどの２つのマスもその中点に星があるものです。複数解の場合に適当に選んだ二つの解の差分に注目することでこのループを作り出すことが常にできます。星が二つの場合、星の座標をrA、rBとするとループは２ノード進むたびに2(rA-rB)だけ並進します。偶数(2n, n>0)ノードでループが閉じるためには2n(rA-rB)がゼロベクトルである必要があります。これは不可能なので二つの星ではループが作れません。したがって星２つでは複数解になりえません。
これは印象的な構造です。たまに見かけます。
３ブロック以上の川だとこのように外側に少しだけひねりが入った形で見ることが多くなります。
このあたりも覚えておいて損はないと思います。
もっと沢山の星からなる空間処理も覚えていく、ということを考えるのも面白い挑戦かと思います。
USBe様の記事で空間処理の逆と呼ばれていたものを天体ショーでも考えることができます。
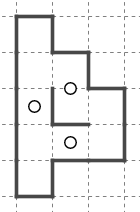
例えばこの形は破綻します。
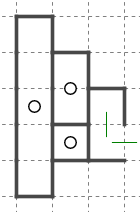
３つのクラスタがありますが、どれか一つに出入り口が出来て大域系とつながると、上に挙げた破綻形にならないように形が確定します。
例えばこれは右下に出入り口が出来た場合です。
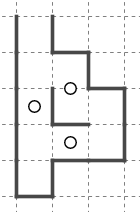
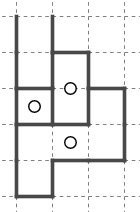
一方、上に出入り口が出来るとこのようになります。
この例はパリティ手筋の変則的な形態としても解釈できます。
空間処理の逆は、破綻形をあえて覚えることで解きを効率化する手法になります。ただし天体ショーの場合は発生がないので破綻形が無数にあります。
あまり理論の整理が出来ていないのですが、私がここまでで記述してきた分類と照らし合わせると、空間処理の逆は破綻閉じ込めや鎖国を含む広い考え方かと思います。広義の迷子の脱出もこれに含まれるかもしれません。準孤立領域がトリガーとなるユニークネス手筋も、広義の、空間処理の逆に含まれると言えるかもしれません。
例えばこの形は破綻します。
３つのクラスタがありますが、どれか一つに出入り口が出来て大域系とつながると、上に挙げた破綻形にならないように形が確定します。
例えばこれは右下に出入り口が出来た場合です。
一方、上に出入り口が出来るとこのようになります。
この例はパリティ手筋の変則的な形態としても解釈できます。
空間処理の逆は、破綻形をあえて覚えることで解きを効率化する手法になります。ただし天体ショーの場合は発生がないので破綻形が無数にあります。
あまり理論の整理が出来ていないのですが、私がここまでで記述してきた分類と照らし合わせると、空間処理の逆は破綻閉じ込めや鎖国を含む広い考え方かと思います。広義の迷子の脱出もこれに含まれるかもしれません。準孤立領域がトリガーとなるユニークネス手筋も、広義の、空間処理の逆に含まれると言えるかもしれません。
天体ショーにおける最終的なゴールは絵を特定することにあります。
したがって必ずしも全てのブロック形状を特定する必要はない、という考え方もできます。
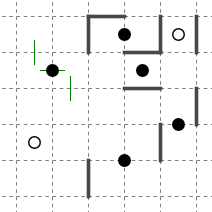
このような状態を考えます。
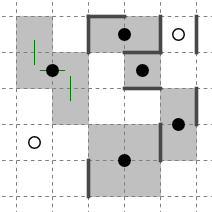
灰色で塗った部分は既に黒になることが確定しています。
中央にどのブロックに入るか決まっていないクラスタが残っていますが、そのクラスタ内のマスがどのブロックに入ろうとも、いずれにせよ黒になることがわかります。
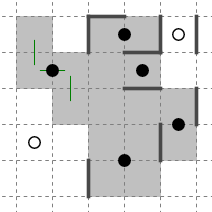
したがってこの状態まで色を決定することができます。
多くの場合、天体ショーの「本質的な」目的をどう解釈するかによって作業量は大きく異なります。この記事では私の普段の解釈である、領域分割パズルとしての側面を記述してきましたが、色決定を最重要視する主義の下では天体ショーは二色で塗り分けるパズルになるため、解き方の雰囲気や手筋にも変化が生じると思われます。
したがって必ずしも全てのブロック形状を特定する必要はない、という考え方もできます。
このような状態を考えます。
灰色で塗った部分は既に黒になることが確定しています。
中央にどのブロックに入るか決まっていないクラスタが残っていますが、そのクラスタ内のマスがどのブロックに入ろうとも、いずれにせよ黒になることがわかります。
したがってこの状態まで色を決定することができます。
多くの場合、天体ショーの「本質的な」目的をどう解釈するかによって作業量は大きく異なります。この記事では私の普段の解釈である、領域分割パズルとしての側面を記述してきましたが、色決定を最重要視する主義の下では天体ショーは二色で塗り分けるパズルになるため、解き方の雰囲気や手筋にも変化が生じると思われます。
例えば「7かける9を計算する方法を説明して下さい」と言われても説明の仕方は千差万別です。
同じように、パズルの解き筋、手筋を説明する方法も沢山あるかと思います。一つの理解の仕方だけでなく多面的に捉えることで理解が深まるかと思います。ここでは私が普段よく使用しているマスベースの解釈を中心に記述しましたが、例えば線ベースの解釈でも深めることができるように思います。
また、ある程度解釈の方向性を絞ったとしても手筋は無数にあるものと思っています。何を手筋とみなすか、と言う問題もありますが、面白そうな手筋が思い当ったら随時追加します。これを追加して欲しい、追加したらどうか、というのがあればご教授いただければと思います。
同じように、パズルの解き筋、手筋を説明する方法も沢山あるかと思います。一つの理解の仕方だけでなく多面的に捉えることで理解が深まるかと思います。ここでは私が普段よく使用しているマスベースの解釈を中心に記述しましたが、例えば線ベースの解釈でも深めることができるように思います。
また、ある程度解釈の方向性を絞ったとしても手筋は無数にあるものと思っています。何を手筋とみなすか、と言う問題もありますが、面白そうな手筋が思い当ったら随時追加します。これを追加して欲しい、追加したらどうか、というのがあればご教授いただければと思います。
パズル用語や手筋分類の参考のために以下に示すサイト群を参考にいたしました。
gesaku >>>>ON<<<< the blog
スリリンの作り方 - とおんきごうのブログ
ぬりかべ
へやわけのできるまで・その１ - air-pupa
続・半袖の隠れ家
フィルオミノでおもうこと。
ニコリのパズル「ましゅ」の解法
裏ましゅ 隠れ○
超上級手筋集１ | ニコリパズル道場！
また、2018年のアドベントカレンダーの記事をいくつか参考にいたしました。
ペンシルパズル Advent Calendar 2018
ペンパWikiの他のページも参考にいたしました。
gesaku >>>>ON<<<< the blog
スリリンの作り方 - とおんきごうのブログ
ぬりかべ
へやわけのできるまで・その１ - air-pupa
続・半袖の隠れ家
フィルオミノでおもうこと。
ニコリのパズル「ましゅ」の解法
裏ましゅ 隠れ○
超上級手筋集１ | ニコリパズル道場！
また、2018年のアドベントカレンダーの記事をいくつか参考にいたしました。
ペンシルパズル Advent Calendar 2018
ペンパWikiの他のページも参考にいたしました。
